Area bounded between two hyperbolas
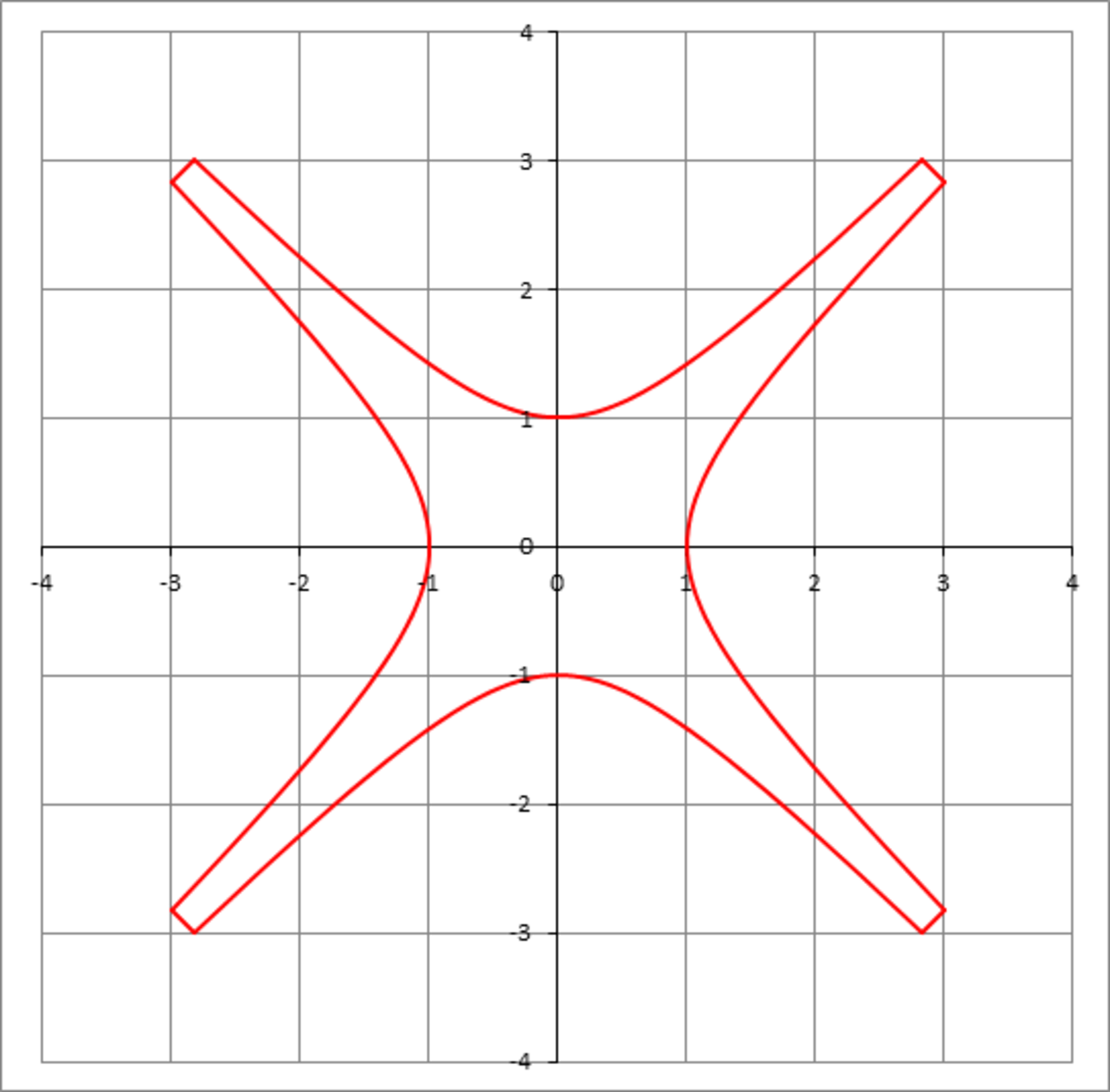
The figure above shows the graphs of and . The graphs are limited to and . The adjacent free ends of the hyperbolas are jointed with straight line segments that have a slope of . Find the area bounded by the hyperbolas and the four line segments.
The answer is 9.05.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It's easiest to picture this hyperbolic figure as being inscribed in a square of side length 6 ⇒ x , y ∈ [ − 3 , 3 ] . Knowing that y 2 − x 2 = 1 intersects the line y = 3 ⇒ x = ± 2 2 , and the chamfered ends are right-isosceles triangles of side length 3 − 2 2 , the required (and highly-symmetric) area computes according to:
A = 6 2 − 4 ∫ − 2 2 2 2 3 − x 2 + 1 d x − 4 [ 2 1 ( 3 − 2 2 ) 2 ] ≈ 9 . 0 5 .