Square Formed From Intersecting Arcs
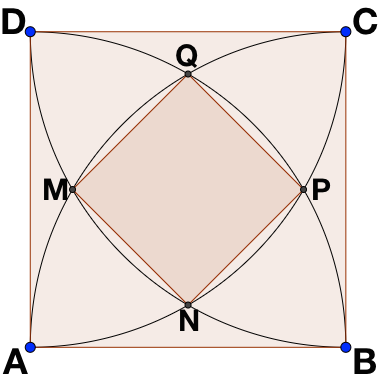
It is given that the area of square A B C D is 6 + 3 3 . Find the area of square M N P Q .
Note : Each square's vertex is a circumcentre of a circular arc.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Great question @Milan Milanic ! My only recommendation is making the labels on the figure larger, like so. :)

Log in to reply
Thank you. I guess that enlarging of labels was automatically done already :)
Exactly Same Way
Please let me know how BQ and AQ lenth is a?
Log in to reply
You use the fact that they are a radius.
Alrighty then, will try to give best explanation on that.
Take a look at (quarter) circle with circumcentre A . Every point that lies on circumference of that circle (points: B , P , Q and D ) is on same distance from point A , which is centre of the circle (therefore: segments A B , A P , A Q and A D have the same length).
Now, that goes for (quarter) circle with circumcentre B and for points A , M , Q and C (and appropriate segments).
Therefore, from the first paragraph (not including "Alrighty..." paragraph) we have A B = A Q and from second on we have B A = B Q . Since A B is as same thing as B A , with length a .
I hope that everything is explained now :)
Nice solution, now the area of curved or complete region represented by MNPQ can be evaluated easity too
Log in to reply
Could you post that version of the problem? Thanks!
I solved it a bit differently. To start, I knew the vesica was used to construct equilateral triangles. So, we know the angle QCP, for example, is 60 degrees. So: 9 0 = 6 0 + 2 θ . We quickly find theta is 15. We kind the adjacent side of a right triangle easily: a = s q r t ( 6 + 3 3 ) / 2 ≈ 1 . 6 7 . And we find the hypotenuse: h = 1 . 6 7 / c o s ( 1 5 ) ≈ 1 . 7 3 . Squaring this gives us the answer: 3 .
Your solution is good and I like the way you did it. A bit more trigonometry, but I don't judge. Thanks for sharing it :)
Equation of circle with center at A(0,0)
x^2 + y^2 = r^2 = 6 + 3*sqrt(3) [1]
Equation of circle with center at B(6 + 3*sqrt(3), 0)
(x - 6 - 3 sqrt(3))^2 +y^2 = 6 + 3 sqrt(3) [2]
Subtracting [1] from [2] :
(x - 6 - 3*sqrt(3))^2 - x^2 = 0
Expanding and simplifying:
x^2 - 2 x * sqrt(6 + 3 sqrt(3)) + 6 + 3sqrt(3) - x^2 = 0
6 + 3 * sqrt(3) = 2 * sqrt( 6 + 3*sqrt(3)) * x
x = ( 6 + 3 * sqrt(3))/ 2*sqrt(6 + 3*sqrt(3)) = app. 1.673
Substituting into [1]
y = 2.8978
By reflection across y = x a second point is:
x = 2.8978 y = 1.673
Distance formula yields length of side = 1.7321
Area = 1.7321^2 = 3
Very nicely explained. That is solved using analytical geometry (if I guessed the name correctly, non-native english speaker). Thank you for revealing and explaining your solution. :)
Tip: If you don't mind, you can use latex, so that your explanations will be more clear in future. When you want to use latex, you type this: \ ( and when you want to finish it, type this: \ ) (both are without spaces between backslash and appropriate bracket). But that can be a drag sometimes. Also, you can check this latex-helper on the link bellow. http://s1.daumcdn.net/editor/fp/service nc/pencil/Pencil chromestore.html
The way i did it was by forming an equilateral triangle, solving for the area of the sectors and then solving for the arrow shapes and so forth. I was left with a reuleauxish type square in the centre with an area of 3.52. I then let A denote the side of the square MNPQ, substituting the values of 3,2 and 1 seeing which one would equal (6+3*(sqrt3)), and three was the answer
Moderator note:
Unfortunately, your solution doesn't offer enough specific details, for me to comment on it. For example, which "rea of sectors and arrow shapes and so forth" did you solve for, and how did you do so?
I'm not sure what the last line meant, especially "substituting the values of 3, 2, and 1 seeing ..."
Take a vertex as origin and side length a and find two of the points on the square by solving quarter circle double equations. Knowing the side or required square in terms of a, area can be easily calculated. The two points are (asin30,acos30) and (asin60,acos60).
Excellent problem! Thank you!
make a line between point Q&A,P&A,project a 90° line form p to AB let us call intersection point z&connect point A to median point of line PQ call it( u),at∆ pzA sin(mAp)=opposite \hypotenuse,opp=square side\2,hypotenuse=square side =Ap (radius ),so sin(mAP)=square side\2÷square side =.5,angle=30°,at∆cAB angle (cAB)=45°,so angle (pau)=45-30=15°,from symmetry angle (pAQ)=15×2=30°,from geometry of ∆PAQ,cos30=PA^2+QA^2- PQ^2 (2×PA×QA),pa=qa=square side ,cos30=2(PA)^2-(PQ^2)\2PA^2, √3\2×2×(6+3√3)=2×(6+3√3)-PQ^2 ,,,,,,,,,,,,pQ^2 =required area =12+6√3 -6√3-9=3
I don't have the heart to leave this without solution. So...
Solution:
Let a be a length of the bigger square's edge. Now, let's concentrate on point Q (or: M , N or P , conclusion will be the same). I believe, that it can be spotted that B Q and A Q length is a . Therefore, triangle A B Q is equilateral. E and F shall be midpoints of A B and C D , respectively. Length of E Q is 2 a 3 , E Q + Q F is a , therefore Q F = a ( 1 − 2 3 ) .
Finally, we can calculate Q N ( N E = Q R , Q N = a − Q R − N E ), which is a ( 3 − 1 ) . Q N and M P both are equal and are M N P Q 's diagonals. Using formula 2 d 2 we will get that area of M N P Q is a 2 ( 2 − 3 ) . Since a 2 is A B C D 's area, we get 3 ( 2 + 3 ) ( 2 − 3 ) which is 3 .