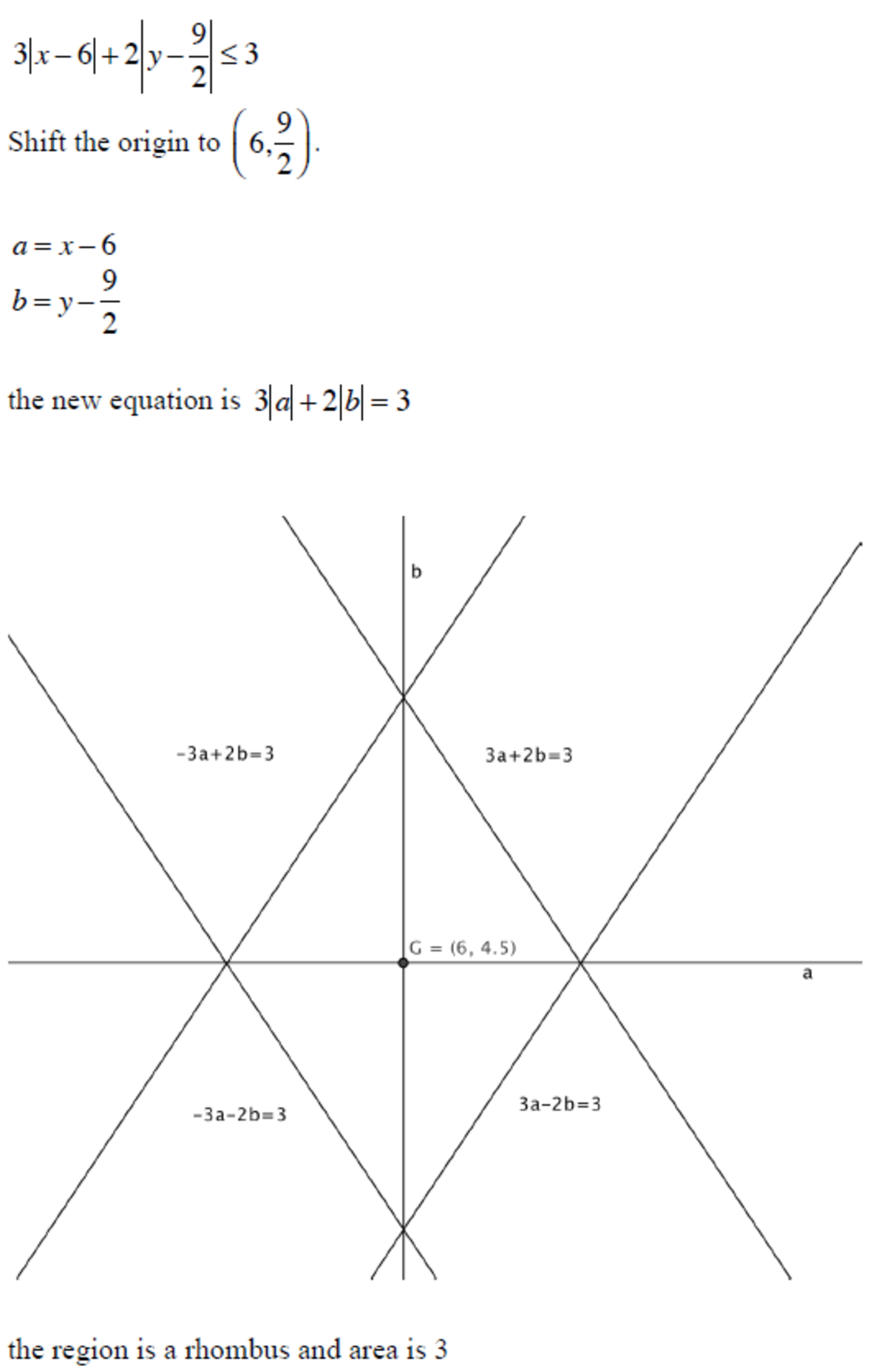
Area defined by Inequality

I found it helpful to draw a sketch graph as I worked out the solution.

Let's start by finding the equations of the lines along which equality holds, in other words where -

$|3x-18|+|9-2y|=3$

This allows us to write down four equations for the four lines bounding the region we are looking for $(3x-18)+(9-2y)=3$

$(3x-18)-(9-2y)=3$

$-(3x-18)+(9-2y)=3$

$-(3x-18)-(9-2y)=3$

Solving the first and second of these as simultaneous equations gives their intersection point $(7,\frac{9}{2})$

Solving the first and third gives their intersection point $(6,3)$

Solving the second and fourth gives their intersection point $(6,6)$

Solving the fourth and third gives their intersection point $(5,\frac{9}{2})$

Plotting these points reveals that the required region is a diamond shape. If you think of it as two identical triangles base to base it is easy to calculate its area as $2\times\frac{1}{2}\times2\times\frac{3}{2}=3$

Note: There is a more sophisticated way to find the vertices of the region, based on the observation that they occur when the argument of one of the modulus functions change sign.