Area Enclosed by Cevians
In △ A B C , we construct three cevians A D , B E , and C F , where the points D , E , F satisfy B D = r B C , C E = r C A , A F = r A B , for some real r , 0 < r < 1 . The three cevians intersect at three points which are the vertices of a triangle which I will call the intersection triangle. Suppose the area of △ A B C = 1 . Take r = 0 . 3 and find the area of the shaded region. Now find the other value of r that will result in the same area of the corresponding intersection triangle.
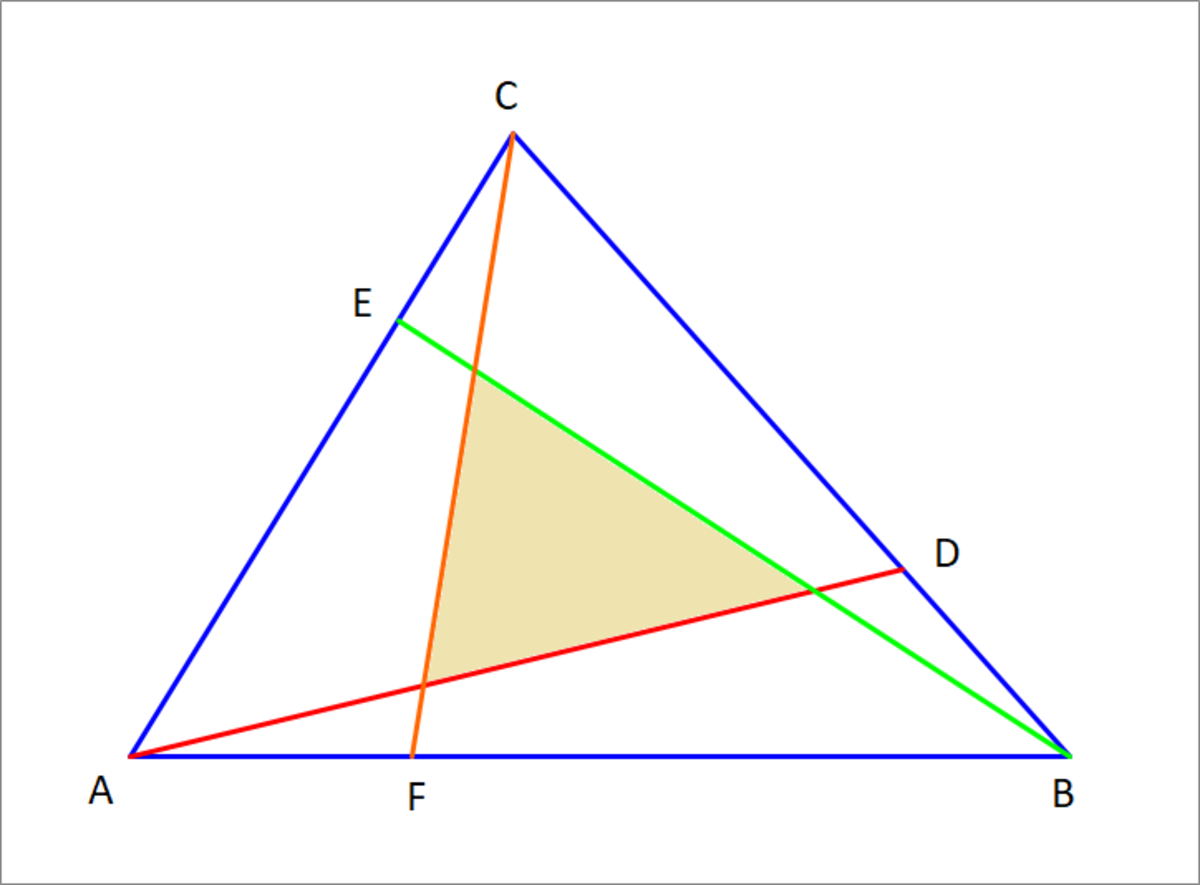
The answer is 0.7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
We can find the ratio of the area of "intersection" triangle to that of the large triangle A B C is given by Routh's theorem . If B D C D = x , C E A E = y , and A F B F = z , then the ratio of areas is given by:
ρ = ( x y + y + 1 ) ( y z + z + 1 ) ( z x + x + 1 ) ( x y z − 1 ) 2
For this problem x = y = z = 0 . 7 0 . 3 = 7 3 . If take the reciprocals of x , y , and z , the area of both triangles do not change, therefore, x 1 = y 1 = z 1 = 3 7 gives the same ρ , therefore the other r = 0 . 7 .
In this solution we are going to use Rouths theorem .
This theorem is only concerned of the area of the original triangle and taking the ratios in some particular orientation (clockwise or anticlockwise) And now since we can look at the same triangle other way around.
so,The answer is 1 − r
The OP has edited the statement....
It can shown that the intersection area is given by
[ A B C ] Area = r 2 − r + 1 ( 1 − 2 r ) 2 = ( r − 2 1 ) 2 + 4 3 4 ( r − 2 1 ) 2
And as such, the area is a function of ( r − 2 1 ) 2 , thus values that are symmetric about r = 2 1 will result in the same area.
In this problem, we started with r = 0 . 3 which is 0 . 2 away from 0 . 5 , thus the other value is 0 . 5 + 0 . 2 = 0 . 7 .