Area in a Triangle
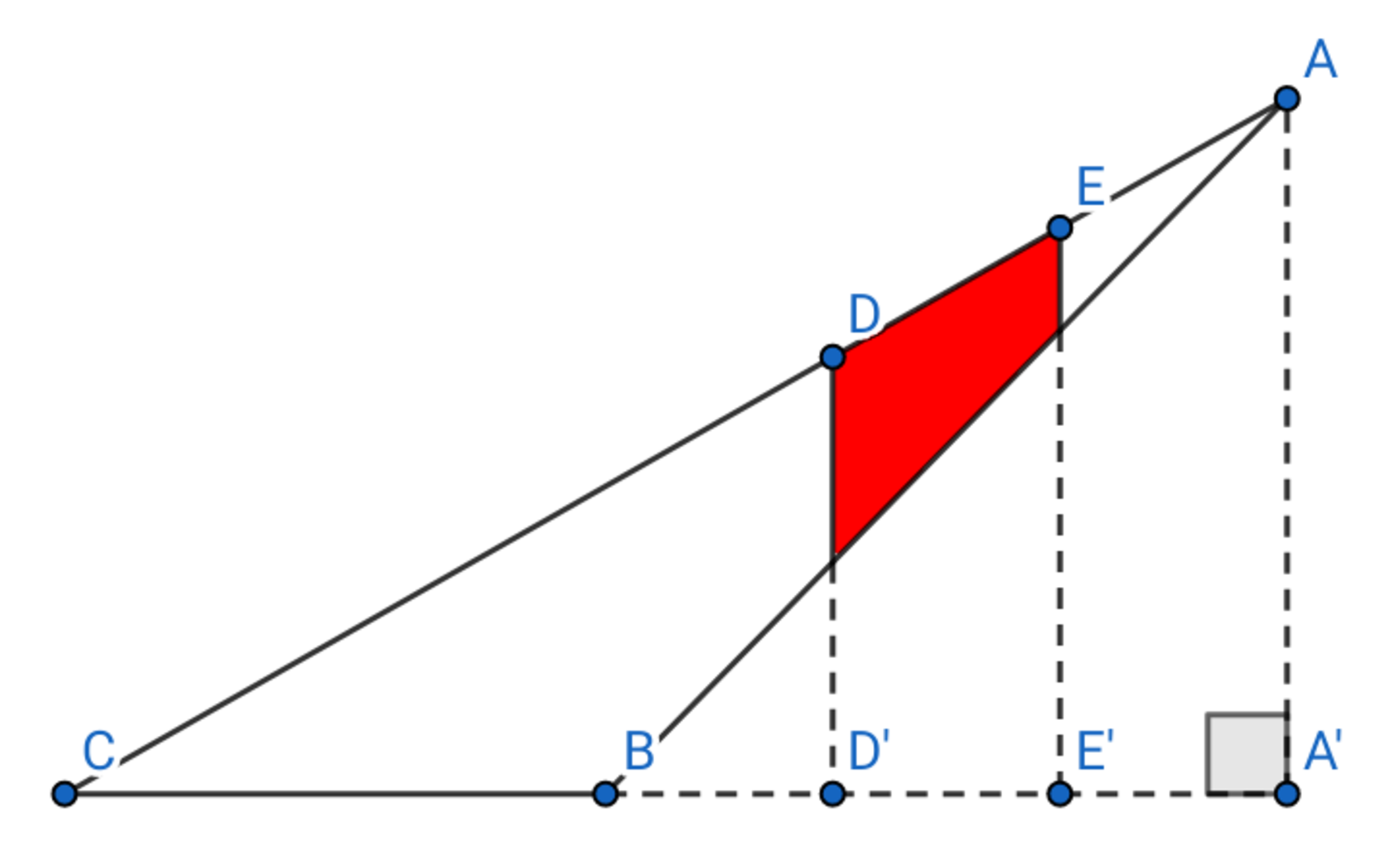
All line segments except for A B and C A are horizontal and vertical lines respectively.
A B = 9 , B C = 5 , and C A = 1 3 . The line segments B D ′ , D ′ E ′ , and E ′ A ′ each has the length one-third of the line segment B A ′ . Let the ratio of the area of the red quadrilateral over the area of △ A B C be x . Which is true about the value of x ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The area of △ A B C is 4 9 5 1 . Since line segments B D ′ , D ′ E ′ , and E ′ A ′ each has the length one-third of the line segment B A ′ , line segments A G , G F , and F B must have lengths one-third of A B , which would make them equal to 3 .
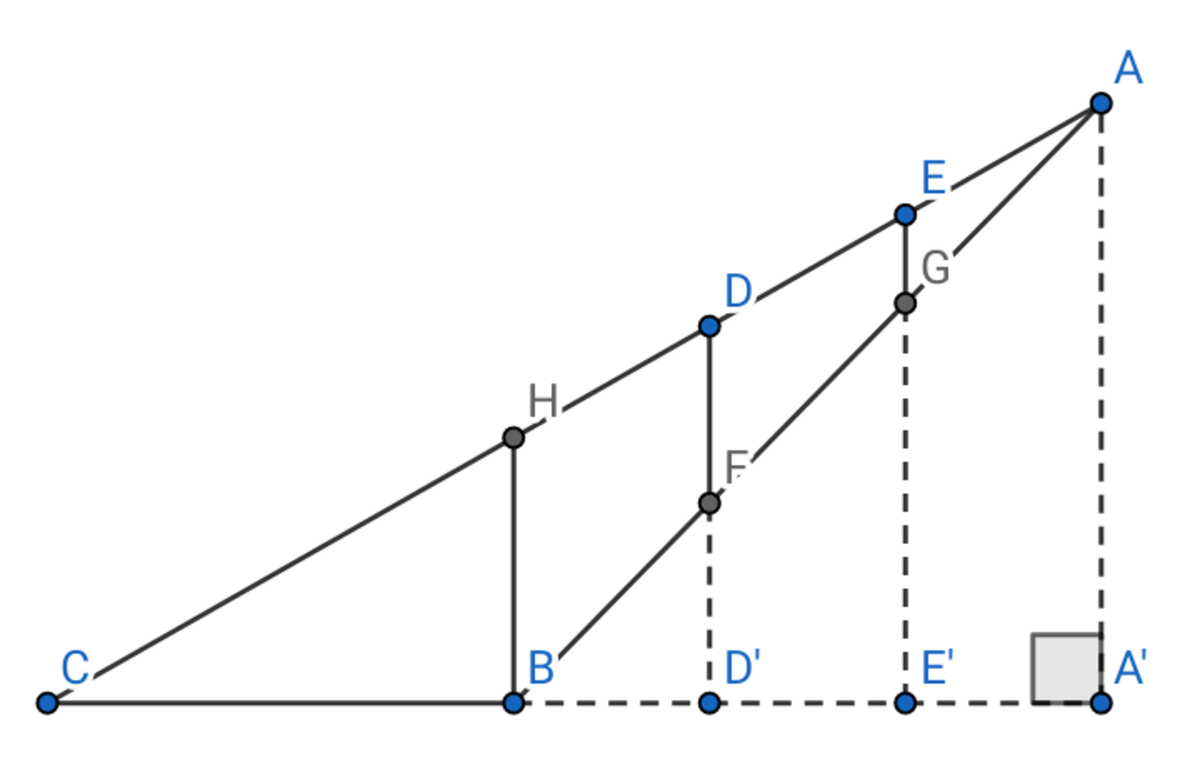
We notice that triangles A B H , A F D , and A G E are all similar. Since area of △ A B H area of △ A F D = A B 2 A F 2 = 9 4 and area of △ A B H area of △ A G E = A B 2 A G 2 = 9 1 because of a theorem of similar triangles , the area of the red shape is only one-third of the area of △ A B H .
Through the use of Law of Cosines , we find that B H = 1 1 3 4 5 5 1 and H A = 1 1 3 8 1 9 . Then the area of triangle A B H is 4 5 2 5 6 7 5 1 and one-third of that is 4 5 2 1 8 9 5 1 which is the area of the red shape.
area of △ A B C area of D E G F = 4 9 5 1 4 5 2 1 8 9 5 1 = 4 0 6 8 5 1 7 5 6 5 1 = 1 1 3 2 1 ≈ 0 . 1 8 5 8 4
Thus, 1 8 . 5 % < x < 1 9 % .
Let A A ′ = h and B D ′ = D ′ E ′ = D ′ A ′ = a . Then we have:
{ A B : C A : h 2 + ( 3 a ) 2 = 9 2 h 2 + ( 3 a + 5 ) 2 = 1 3 2 . . . ( 1 ) . . . ( 2 ) ⟹ ( 2 ) − ( 1 ) : 3 0 a + 2 5 = 8 8 ⟹ a = 2 . 1
The area of △ A B C , [ A B C ] = 2 B C ⋅ h = 2 . 5 h . The area of the red region:
[ D E E ′ ′ D ′ ′ ] = [ C E E ′ ] − [ C D D ′ ] − [ D ′ D ′ ′ E ′ ′ E ′ ] = [ C E E ′ ] − [ C D D ′ ] − ( [ B E ′ E ′ ′ ] − [ B D ′ D ′ ′ ] ) = ( 3 a + 5 2 a + 5 ) 2 [ A A ′ C ] − ( 3 a + 5 a + 5 ) 2 [ A A ′ C ] − ( 3 a 2 a ) 2 [ A A ′ B ] + ( 3 a a ) 2 [ A A ′ B ] = ( 3 a + 5 ) 2 ( 2 a + 5 ) 2 − ( a + 5 ) 2 [ A A ′ C ] − 3 2 2 2 − 1 2 [ A A ′ B ] = ( 3 a + 5 ) 2 3 a 2 + 1 0 a ⋅ 2 ( 3 a + 5 ) h − 3 1 ⋅ 2 3 a h = 2 ( 3 a + 5 ) ( 3 a 2 + 1 0 a ) h − 2 a h = 2 2 . 6 3 4 . 2 3 h − 2 2 . 1 h ≈ 0 . 4 6 4 6 h By similar triangles
Therefore x = A B C [ D E E ′ ′ D ′ ′ ] ≈ 2 . 5 h 0 . 4 6 4 6 h ≈ 0 . 1 8 5 8 = 1 8 . 5 8 % . ⟹ 1 8 . 5 % < x < 1 9 % .