Area inside a region
f ( x ) = x + sin ( x ) .
What is the area of one of the infinitely many closed regions between the curves y = f ( x ) and its inverse function y = f − 1 ( x ) ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Shouldn’t the integration be from -pi to pi?
Log in to reply
No, see the image. The region being asked for goes from x=0 to x=pi
The first thing to notice is that that
y
=
f
−
1
(
x
)
⇔
x
=
f
(
y
)
So, let A be the set of points ( x 0 , y 0 ) ∈ { ( x , y ) : y = f ( x ) } and B be the set of points ( x 0 , y 0 ) ∈ { ( x , y ) : y = f − 1 ( x ) } .
With that in mind, it is possible to conclude that ( x 0 , y 0 ) ∈ B ⇔ ( x 0 , y 0 ) ∈ { ( x , y ) : x = f ( y ) }
( x 0 , y 0 ) ∈ B ⇔ ( y 0 , x 0 ) ∈ A
If we want to find the points in which A and B that intersect with each other, we know that ( x 0 , y 0 ) ∈ B , ( x 0 , y 0 ) ∈ A , which implies ( y 0 , x 0 ) ∈ A , ( x 0 , y 0 ) ∈ A . So, x 0 = y 0 .
So if y = f ( x ) = f − 1 ( x ) , then y = x
In this case, x + s i n ( x ) = x
s i n ( x ) = 0
x = k π , k is an integer.
If we want one region, let us just take two adjacent points belonging in A and B , say x = 0 and x = π . We know that since both curves are continuous, there must be a closed region in the interval between 0 and π .
It is important to notice that the two are a reflection of each other with respect to the line y = x .
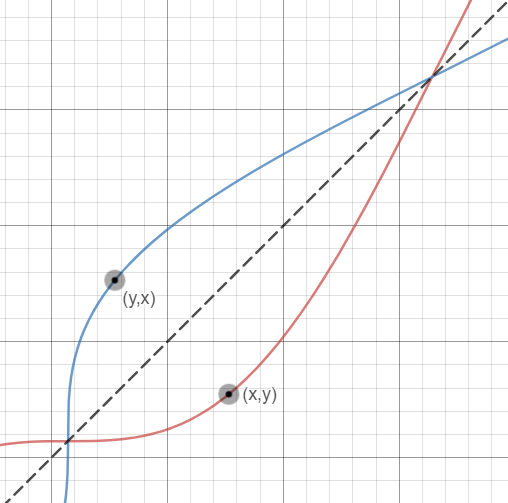
That makes it easier for us to calculate, since it is clear that the area between y = x and y = f ( x ) = x + s i n ( x ) is always half the area of the region.
2 A = ∥ ∫ 0 π ( f ( x ) − x ) d x ∥ = ∫ 0 π ( ( s i n ( x ) + x ) − x ) d x = ∫ 0 π s i n ( x ) d x = 2 ⇒ A = 2 × 2 = 4
I think you meant y = f^(-1)(x) for B, right?
The inverse of f(x) = x + sin x exists and satisfies x = y + sin y. Interestingly, y is indeed a function of x in this second equation but it appears impossible to solve for y explicitly in terms of x. Am I missing something? This is a nuance I've not encountered before...
Log in to reply
Functions can be defined however you want them to be defined. For example, if I wanted a function of x to be 0 if x is rational, and 1 if x is irrational, that would totally be a valid function, although it is impossible to really draw it.
The same thing goes for this f − 1 ( x ) . Let's call it g ( x ) , for the sake of simplicity. One way of defining it is that g ( x + s i n ( x ) ) = x . It impossible explicitly define it through elementary functions (algebraic, trigonometric, log/exponential functions), but you can actually make a curve out of it. One example of a curve that works a bit like that would be the function that tells the area, from minus infinity to x, of a gaussian bell curve. It is something proven to be impossible to write as a composition of elementary functions, and still we find numerical approximations for it because of its importance in statistics and other fields.
Log in to reply
Yes, piecewise defined functions, accumulation functions etc. are all defined their own way. What's different here, I think, is that f(x) itself is defined as the sum of two elementary functions, yet it's inverse apparently can not be solved for y using standard elementary functions. Unless new notation is introduced, (as with inverse trig and log functions), we're essentially stuck with an implicit relationship here.
You are correct in that it is impossible to solve explicitly for y in terms of x. Check out the 'Kepler's Equation' entry on wikipedia to see how to numerically approximate the inverse or find a taylor expansion that describes this particular transcendental function. As for me, I solved this problem numerically, but Rafael's answer is better by far.
Thanks for the Wikipedia reference...Taylor Series did (briefly) cross my mind with this..
If f ( x ) = f − 1 ( x ) , then immediately follows that f ( x ) = x ∧ f − 1 ( x ) = x (for the values of x at intersections of those two functions), which is obvious if you think about it: the inverse function is the function of x mirrored in the line y = x and intersections between the function and the inverse of that same function will be on the line y = x because on those points the mirrored point will be at the same spot. So we can immediately conclude that f ( x ) = x and thus s i n ( x ) = 0 which implies that x = k ⋅ π ∣ k ∈ Z
Now we know for which x there will be a intersection, we will just need two following values for x . Let's take x = 0 and x = π , for example. We can use that the area within the function and the inverse of that function for 0 ≤ x ≤ π will be 2 ⋅ ∣ ∫ 0 π ( f ( x ) − x ) d x ∣ . This is because the area between the two functions is double the area of f ( x ) to the line y = x , because the inverse function still is mirrored in the line y = x .
This means that the asked area has to be 2 ⋅ ∣ ∫ 0 π ( s i n ( x ) + x − x ) d x ∣ = 2 ⋅ ∣ ∫ 0 π ( s i n ( x ) ) d x ∣ = 2 ⋅ ∣ [ − c o s ( x ) ] 0 π ∣ = 2 ⋅ ∣ 1 − ( − 1 ) ∣ = 2 ⋅ 2 = 4
Consider the following graph:

Where we present (red) f ( x ) and (blue) f − 1 ( x ) trapped inside a square of side π . (The two intersections happen at ( 0 , 0 ) , ( π , π ) ). It is clear that ∫ 0 π x + sin x d x = B + C so B + C = 2 π 2 − 2 . But we know that A + B + C = π 2 and because of a symmetry argument already presented in another solution, C = A so we have the system 2 A + B = π 2 B + A = 2 π 2 − 2 It is solvable and we really just care for B = 4 .

An taking the inverse of a function is same as reflection of its graph along the y=x axis. So the area would be the twice the value of the area between the curve and the line y=x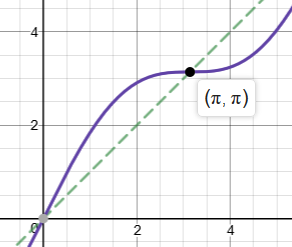 A
=
2
×
∫
0
π
x
+
s
i
n
(
x
)
d
x
−
π
2
=
4
A
=
2
×
∫
0
π
x
+
s
i
n
(
x
)
d
x
−
π
2
=
4