Area of a circular sector

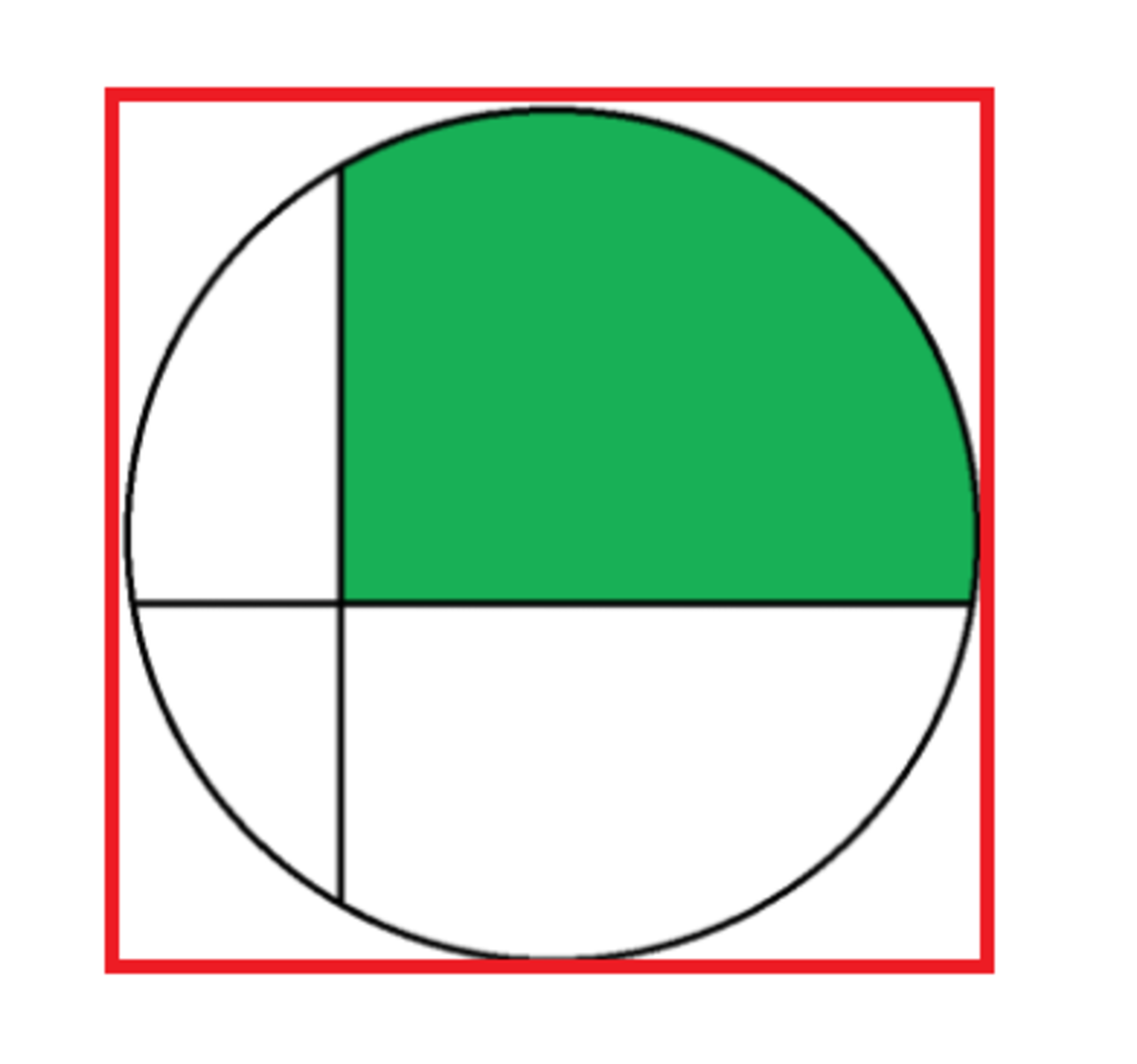
A circle is centered at the origin with a radius of 5. Two lines are drawn intersecting the circle, the first is the line y = − 1 , and the other is x = − 3 . Their intersection forms four sectors. Find the area of the sector shaded in green.
The answer is 41.645.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since this is a hybrid calculus / geometry problem, let's explore an interesting question: Can we effectively do calculus without actually doing any calculus? We can, with Monte Carlo integration. What's even better is that we don't have to figure out where the lines intersect the circle. Here's the process:
1)
Generate
x
y
points randomly (with uniform distribution) within a square region circumscribing the circle. Generate a great many such points.
2)
Keep a count of the number of points falling within the circle
(
x
2
+
y
2
≤
R
2
)
3)
Also keep count of the number of points within the green region. Note that this is just Condition 2 plus
(
x
≥
−
3
)
and
(
y
≥
−
1
)
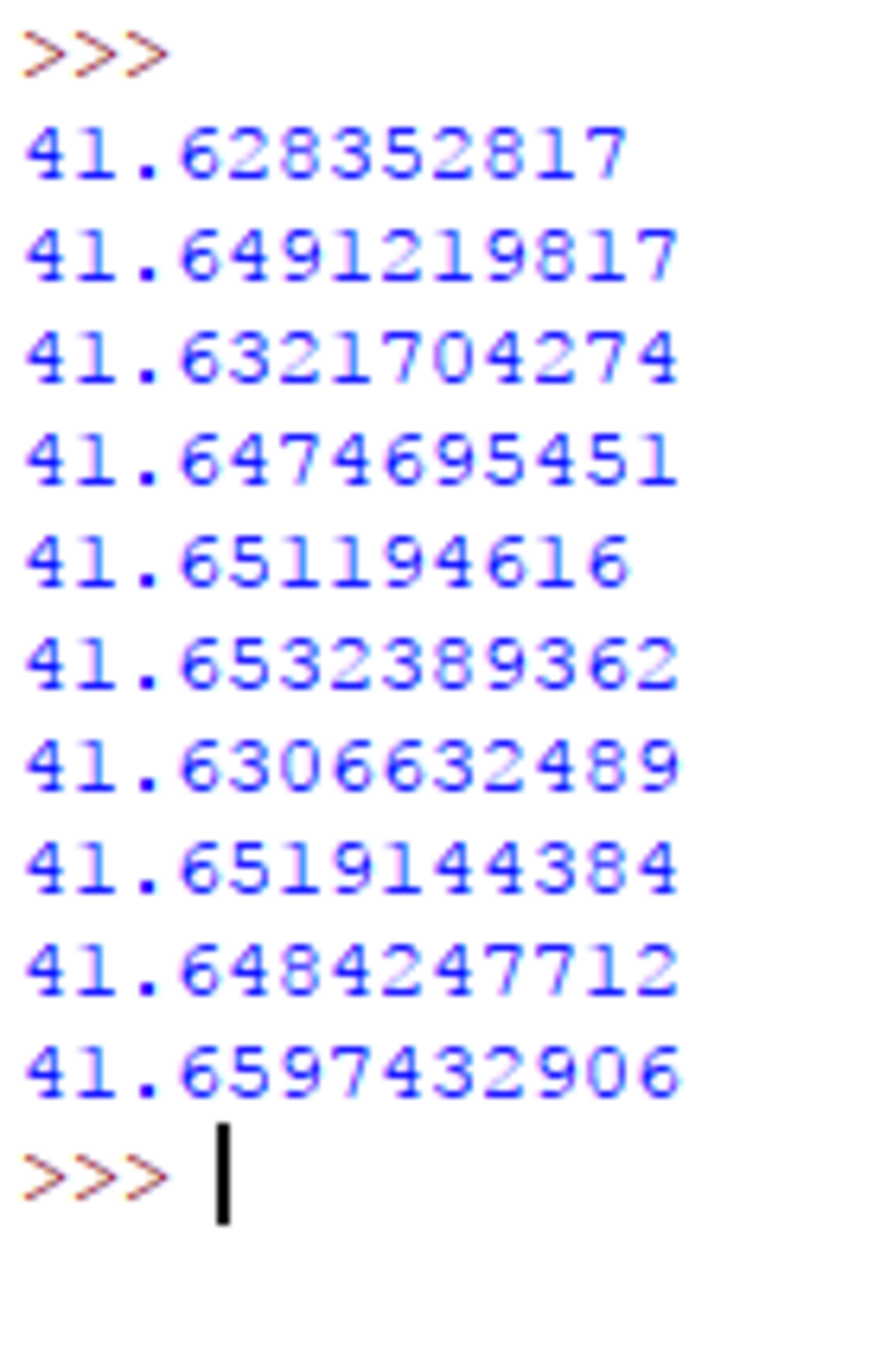
The ratio of the counts from (3) to the counts from (2) is approximately the ratio of the green area to the circle area. Then we can multiply the ratio by the circle area to get the final answer. With a large number of points, we get reasonably good results (see below).
import math
import random
for q in range(0,10): # 10 trials with 10^7 points each
R = 5.0
Count_circle = 0
Count_green = 0
N = 10**7
######################################################
for j in range(0,N):
circ_flag = 0
x = random.uniform(-R,R) # Random xy in square circumscribing circle
y = random.uniform(-R,R)
if x**2.0 + y**2.0 <= R**2.0: # "In circle" check
Count_circle = Count_circle + 1
circ_flag = 1
if (circ_flag == 1) and (x >= -3.0) and (y >= -1.0): # "In green" check
Count_green = Count_green + 1
######################################################
ratio = float(Count_green) / float(Count_circle) # Count ratio = area ratio
A_circle = math.pi * R**2.0
A_green = ratio * A_circle
######################################################
print A_green
Points on the circle are given in parametric form by
( x ( t ) , y ( t ) ) = ( 5 cos ( t ) , 5 sin ( t ) )
We first find the value of t corresponding to the intersection of the first line y = − 1 with the circle, It is straight forward to find that
t 1 = sin − 1 ( 5 − 1 )
Similarly, intersecting the circle with the line x = − 3 , results in
t 2 = cos − 1 ( 5 − 3 )
The point of intersection of the two lines is p 0 = ( − 3 , − 1 )
Relative to this point (that is, by taking this point p 0 to be the new origin ), then the position of the a point on the circle is given by
( x ( t ) , y ( t ) ) = ( 5 cos t + 3 , 5 sin t + 1 )
Finally, we can use the following formula for find the area of a parametric curve between t = t 1 and t = t 2
Area = 2 1 ∫ t 1 t 2 x ( t ) y ′ ( t ) − y ( t ) x ′ ( t ) d t
Plugging in x ( t ) and y ( t ) into this formula, we obtain,
Area = 2 1 ∫ t 1 t 2 ( ( 3 + 5 cos t ) ( 5 cos t ) − ( 1 + 5 sin t ) ( − 5 sin t ) ) d t = 2 1 ∫ t 1 t 2 ( 2 5 + 1 5 cos t + 5 sin t ) d t = 2 1 ( 2 5 t + 1 5 sin t − 5 cos t ) ∣ t 1 t 2 = 2 1 ( 2 5 ( t 2 − t 1 ) + 1 5 ( sin t 2 − sin t 1 ) − 5 ( cos t 2 − cos t 1 ) )
Pluggin in the values of t 1 and t 2 in the above expression, we obtain
Area = 4 1 . 6 4 5
This problem can be solved without using calculus:
The equation of the circle:
x 2 + y 2 = 2 5
Substituting x = -3 and then y = -1 gets us the coordinates of the two endpoints of the arc bordering the green area:
A ( − 3 , − 4 ) and B ( 2 4 , − 1 )
Now, if we draw the coordinate axes and connect the origin with the points A and B, these lines divide the green area into a quarter of our circle (25π/4), a rectangle (1 × 3 = 3), two right angled triangles (areas: 3×4/2 = 6 and 1×√(24) / 2 = √6) and two sectors (where the central angles are a and b, and tan(a) = 3/4 and tan(b) = 1 / √ (24) .
(I would appreciate a diagram from someone.)
Hence the total green area:
G = 4 2 5 π + 3 + 6 + 6 + 3 6 0 ° arctan ( 4 3 ) + arctan ( 2 4 1 ) × 2 5 π = 4 1 . 6 4 5 (3 d. p.)