Area of a composite figure

Geometry Level 1

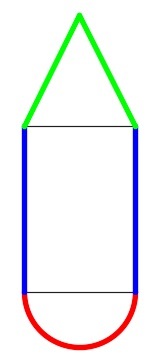The composite figure shown above is composed of a semi-circle (colored red), a rectangle (colored blue), and an isosceles triangle (colored green). The longer side of the rectangle is three times the radius of the semi-circle. The altitude of the triangle is twice the radius of the semi-circle. If the area of the triangle is 20, find the area of this composite figure. Give your answer as a decimal number rounded to three decimal places.


The answer is 95.708.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Tom Engelsman
Aug 12, 2018

If r r equals the radius of the semi-circle, then we have the following area formulas:

Semi-circle = π 2 r 2 \frac{\pi}{2} r^2 , Rectangle = ( 2 r ) ( 3 r ) = 6 r 2 (2r)(3r) = 6r^2 , Triangle = 1 2 ( 2 r ) 2 = 2 r 2 \frac{1}{2}(2r)^2 = 2r^2

and the total area of this composite figure equals π 2 r 2 + 6 r 2 + 2 r 2 = ( 8 + π 2 ) r 2 . \frac{\pi}{2}r^2 + 6r^2 + 2r^2 = (8 + \frac{\pi}{2})r^2.

If the area of the triangle equals 20, then we obtain r 2 = 10 r^2 = 10 and ultimately ( 8 + π 2 ) r 2 = ( 8 + π 2 ) ( 10 ) = 95.708 . (8 + \frac{\pi}{2})r^2 = (8 + \frac{\pi}{2})(10) = \boxed{95.708}.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...