Area of a cyclic triangle
Find the area of △ A B C given that:
- The radius of the circle is 1m.
- A B = 1 m
- ∠ C A B = 5 0 ∘
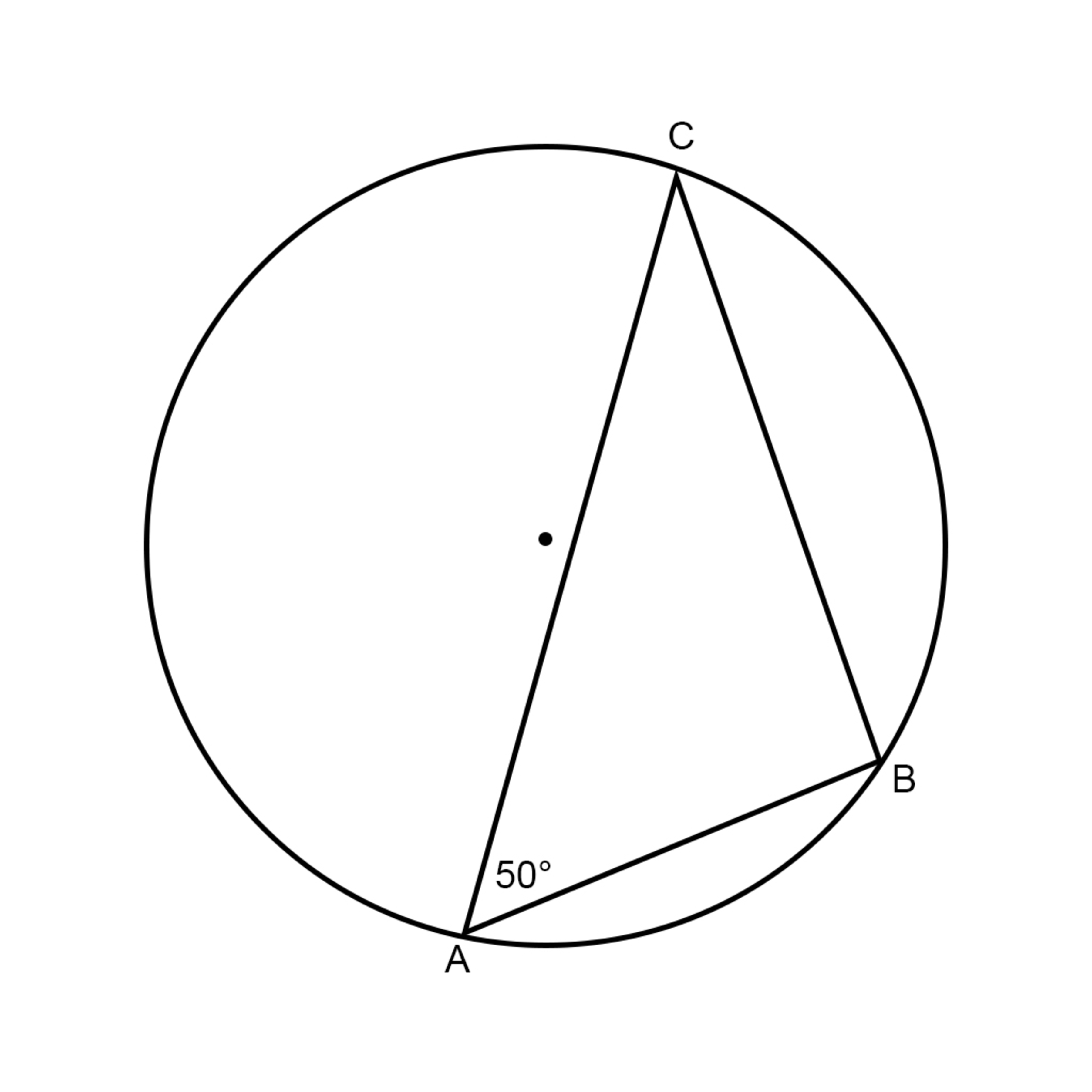
The answer is 0.754406506.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I have to admit, yours is slightly more efficient than mine. Great work!
-
Let O be the center of the circle.
-
OA=OB=AB as they are all radii ∴ △ O A B is equilateral.
-
∠ O A C = 6 0 − ∠ C A B = 1 0 d e g
-
Using the circle theorem "The angle subtended at the centre is twice the angle subtended at the circumference from the same points". ∠ C O B = 2 × ∠ B A C = 1 0 0 d e g
-
△ O B C is issoceles as two sides are radii. Thus, ∠ O B C = ∠ O C B = 2 1 ( 1 8 0 − ∠ C O B ) = 4 0
-
∠ A C B = 4 0 − 1 0 = 3 0 d e g
-
From here, use the sine rule, sin A a = sin B b = sin C c , To work out length BC.
-
B C = sin 3 0 1 × sin 5 0 = 1 . 5 3 2 ( 3 d . p )
-
Now, use 2 1 a b sin C to work out the area.
-
2 1 × 1 . 5 3 2 . . . × 1 × ( 1 8 0 − 5 0 − 3 0 ) = 0 . 7 5 4 4 0 6 5 0 6 m 2
Slightly different approach:
Let O be the center of the circle. Then since O A = O B = A B = 1 , △ O A B is equilateral and ∠ A O B = 6 0 ∘ . Next, ∠ A C B = 2 1 ∠ A O B = 3 0 ∘ as they both subtend arc A B ; this makes ∠ A B C = 1 0 0 ∘ . Using sine law,
A C sin 1 0 0 ∘ A C sin 1 0 0 ∘ A C = 1 sin 3 0 ∘ = 2 1 = 2 sin 1 0 0 ∘
Finally, the area A of △ A B C is
A = 2 1 ( A B ) ( A C ) s i n ∠ B A C = 2 1 ( 1 ) ( 2 sin 1 0 0 ∘ ) sin 5 0 ∘ ≈ 0 . 7 5 4 4 0 6 5 0 6 7 3 5