Area of a derived triangle
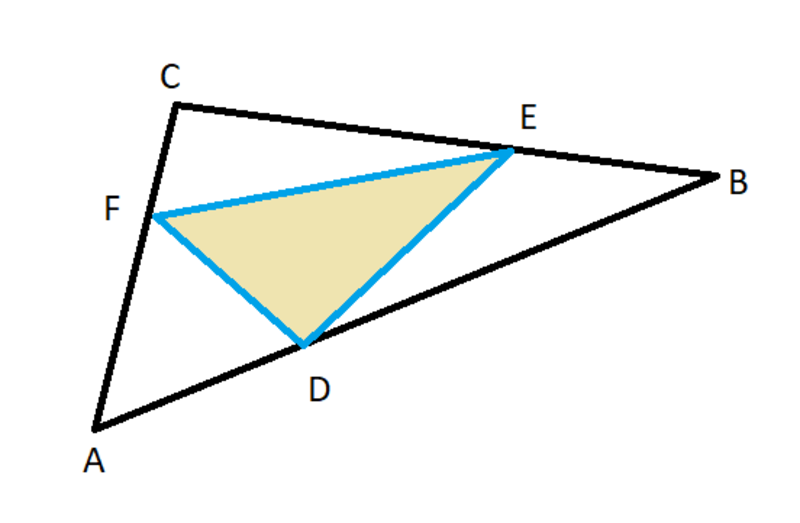
In △ A B C , we place points D , E , and F on sides A B , B C , and C A respectively, such that A B A D = B C B E = C A C F = 3 1 . Find the ratio of the area of △ D E F to the area of △ A B C .
The answer is 0.3333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Since the required ratio is independent of the shape of the triangle A B C , let us take this triangle as a right isosceles triangle, right angled at A . Let the coordinates of A , B and C be ( 0 , 0 ) , ( 3 a , 0 ) and ( 0 , 3 a ) respectively.
Then those of D , E and F are ( a , 0 ) , ( 2 a , a ) and ( 0 , 2 a ) respectively.
So, area of △ D E F is 2 3 a 2 ,
and that of △ A B C is 2 9 a 2
Therefore the required ratio is 1 : 3 ≈ 0 . 3 3 3 3 .
Let the side lengths opposite A , B , and C be a , b , and c ; and the respective altitudes be h a , h b , and h c . Then the area of △ A B C , [ A B C ] = 2 a h a = 2 b h b = 2 c h c .
We note that [ C E F ] = 2 1 ⋅ 3 2 a ⋅ 3 1 h a = 9 a h a = 9 2 [ A B C ] . Similarly [ A D F ] = 9 b h b = 9 2 [ A B C ] and [ B D E ] = 9 c h c = 9 2 [ A B C ] .
Therefore,
[ A B C ] [ D E F ] = [ A B C ] [ A B C ] − [ C E F ] − [ A D F ] − [ B D E ] = 1 − 3 2 = 3 1 ≈ 0 . 3 3 3
△ A B C can be stretched and skewed to an equilateral triangle with a side length of 3 and still preserve the ratio of areas:
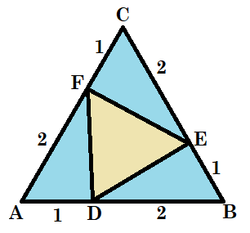
Using the law of cosines on △ A D F , D F = 1 2 + 2 2 − 2 ⋅ 1 ⋅ 2 ⋅ cos 6 0 ° = 3 , and by symmetry △ D E F is also an equilateral triangle.
Since the ratio of sides of the two equilateral triangles is 3 3 , the ratio of their areas is 3 2 3 2 = 3 1 ≈ 0 . 3 3 3 3 .
We have Δ A B C = 2 1 C A ⋅ B C sin C and Δ C E F = 2 1 C E ⋅ C F sin C = 9 1 C A ⋅ B C sin C
so (by symmetry) Δ C E F = Δ B D E = Δ A F D = 9 2 Δ A B C
and Δ D E F = Δ A B C − 3 × 9 2 Δ A B C = 3 1 Δ A B C
so the answer is 3 1 .