Area of a leaf
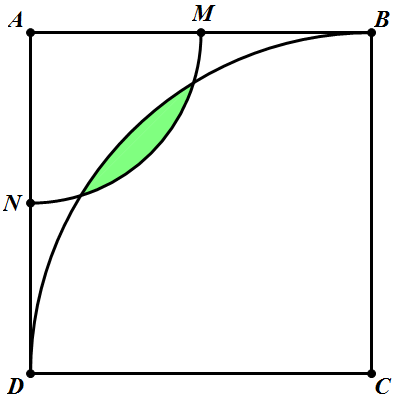
A B C D is a square of side length 2, and M and N are the mid points of sides A B and A D respectively. Construct 2 circles with their center at A and C of radii 1 and 2 respectively.
Find the area of the green region.
The answer is 0.108.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I spent days trying to solve this my self and you're here telling me that there is a rule for such situation LLLLLLLLLLLLLLLLLLLLLLOOOOOOOOOOOOOOOOOOOOOOOOLLLLLLLLLLLLLLLLLLLLLLLLLL
We will tackle this with coordinate geometry and calculus. Let A be the origin, A B the positive x-axis, and A D the negative y-axis. The equation for the circle with center A is y = − 1 − x 2 . The equation for the circle with center C is y = 4 − ( x − 2 ) 2 − 2 . First we must find where they intersect by equating the two equations for the circles. − 1 − x 2 + 2 1 − x 2 − 4 1 − x 2 + 4 − 4 1 − x 2 3 2 x 2 − 4 0 x + 9 = 4 − ( x − 2 ) 2 = − x 2 + 4 x = 4 x − 5 = 0 Solving this quadratic results in our two x-coordinates of intersection, which are 8 5 + 7 and 8 5 − 7 . Now we set up the integral for solving for the area of the leaf where I is the desired integral. I = ∫ 8 5 − 7 8 5 + 7 4 − ( x − 2 ) 2 − 2 + 1 − x 2 d x = ∫ 8 5 − 7 8 5 + 7 4 − ( x − 2 ) 2 d x − 2 ∫ 8 5 − 7 8 5 + 7 d x + ∫ 8 5 − 7 8 5 + 7 1 − x 2 d x Now we will focus on solving the first portion of the integral. = = = = = = = ≈ ∫ 8 5 − 7 8 5 + 7 4 − ( x − 2 ) 2 d x u = x − 2 , d u = d x ∫ 8 5 − 7 8 5 + 7 4 − u 2 d u u = 2 sin ( v ) , d u = 2 cos ( v ) d v 4 ∫ 8 5 − 7 8 5 + 7 cos ( v ) 1 − sin 2 ( v ) d v 4 ∫ 8 5 − 7 8 5 + 7 cos 2 ( v ) d v 2 ∫ 8 5 − 7 8 5 + 7 1 + cos ( 2 v ) d v 2 ( v + 2 1 sin ( 2 v ) ) 2 arcsin ( 2 u ) + sin ( 2 arcsin ( 2 u ) ) 2 arcsin ( 2 x − 2 ) + sin ( 2 arcsin ( 2 x − 2 ) ) ∣ ∣ ∣ ∣ ∣ 8 5 − 7 8 5 + 7 0 . 9 4 4 The second, or trivial, portion of the integral is equal to − 2 7 = − 1 . 3 2 3 . We will now focus on the third portion of the integral. = = = = ≈ ∫ 8 5 − 7 8 5 + 7 1 − x 2 d x x = sin ( u ) , d x = cos ( u ) d u ∫ 8 5 − 7 8 5 + 7 cos 2 ( u ) d u 2 1 ∫ 8 5 − 7 8 5 + 7 1 + cos ( 2 u ) d u 2 1 u + 4 1 sin ( 2 u ) 2 1 arcsin ( x ) + 4 1 sin ( 2 arcsin ( x ) ) ∣ ∣ ∣ ∣ ∣ 8 5 − 7 8 5 + 7 0 . 4 8 7 Finally, adding all portions of the original integral, I , we get 0 . 9 4 4 + 0 . 4 8 7 − 1 . 3 2 3 = 0 . 1 0 8
You cleared all my doubt
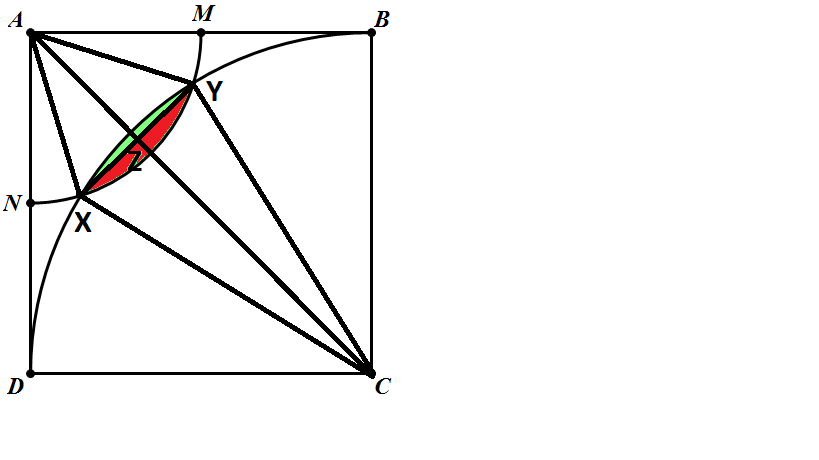 After connecting the points as above in the figure, we know that
A
C
=
2
2
since the side length of the square is 2. Also,
A
X
=
1
and
C
X
=
2
(radii). Now let
A
Z
=
x
, making
C
Z
=
2
2
−
x
and applying the Pythagorean theorem, we get
X
Z
=
(
A
X
)
2
−
(
A
Z
)
2
=
(
C
X
)
2
−
(
C
Z
)
2
and plugging in values
(
1
)
2
−
(
x
)
2
=
(
2
)
2
−
(
2
2
−
x
)
2
and solving further
1
−
x
2
=
4
−
(
8
−
4
x
2
+
x
2
)
1
−
x
2
=
4
−
8
+
4
x
2
−
x
2
1
=
−
4
+
4
x
2
4
2
5
=
x
which simplifies to
x
=
A
Z
=
8
5
2
and
C
Z
=
8
1
1
2
.
After connecting the points as above in the figure, we know that
A
C
=
2
2
since the side length of the square is 2. Also,
A
X
=
1
and
C
X
=
2
(radii). Now let
A
Z
=
x
, making
C
Z
=
2
2
−
x
and applying the Pythagorean theorem, we get
X
Z
=
(
A
X
)
2
−
(
A
Z
)
2
=
(
C
X
)
2
−
(
C
Z
)
2
and plugging in values
(
1
)
2
−
(
x
)
2
=
(
2
)
2
−
(
2
2
−
x
)
2
and solving further
1
−
x
2
=
4
−
(
8
−
4
x
2
+
x
2
)
1
−
x
2
=
4
−
8
+
4
x
2
−
x
2
1
=
−
4
+
4
x
2
4
2
5
=
x
which simplifies to
x
=
A
Z
=
8
5
2
and
C
Z
=
8
1
1
2
.
1 ) For the circle with radius 1, we first find the area of A X Y and subtract the area of △ A X Y from it. To find the area of the sector, first we calculate its angle cos ∠ X A Z = A X A Z or ∠ X A Z = cos − 1 ( 1 8 5 2 ) ≈ 2 7 . 8 8 ∘ and multiply it by two to find the whole angle ∠ X A Z ⋅ 2 = ∠ X A Y ≈ 5 5 . 7 7 ∘
Now we'll find the area of the sector as 3 6 0 ∘ 5 5 . 7 7 ∘ ⋅ π ⋅ ( 1 ) 2 ≈ 0 . 4 8 6 7
To find the area of the triangle, first we know A X = 1 and A Z = 8 5 2 and we find X Z using Pythagorean Theorem X Z = A X 2 − A Z 2 X Z = 1 2 − ( 8 5 2 ) 2 as X Z = 8 1 4 hence the area of △ A X Y = A Z ⋅ X Z △ A X Y = 8 5 2 ⋅ 8 1 4 △ A X Y = 6 4 5 2 8 ≈ 0 . 4 1 3 4 Now the area of the red portion of the green leaf is just 0 . 4 8 6 7 − 0 . 4 1 3 4 = 0 . 0 7 3 3 ⟹ A
2 ) For the circle with radius 2, we first find the area of C X Y and subtract the area of △ C X Y from it as we did above. To find the area of the sector, we calculate cos ∠ X C Z = C X C Z ∠ X C Z = cos − 1 ( 2 8 1 1 2 ) cos − 1 ( 1 6 1 1 2 ) ≈ 1 3 . 5 2 ∘ and multiply it by two to find the whole angle ∠ X C Z ⋅ 2 = ∠ X C Y ≈ 2 7 . 0 4 ∘ Now similar to what we did above, we are going to find the area of the sector by 3 6 0 ∘ 2 7 . 0 4 ∘ ⋅ π ⋅ ( 2 ) 2 ≈ 0 . 9 4 4 2 To find the area of the triangle we will do △ C X Y = C Z ⋅ X Z △ C X Y = 8 1 1 2 ⋅ 8 1 4 △ C X Y = 6 4 1 1 2 8 ≈ 0 . 9 0 9 5 The area of the green portion of the leaf is just 0 . 9 4 4 2 − 0 . 9 0 9 5 = 0 . 0 3 4 7 ⟹ B
The final answer is A + B = 0 . 0 7 3 3 + 0 . 0 3 4 7 ≈ 0 . 1 0 8 .
The area between two overlapping circles is A = r 2 cos − 1 ( 2 d r d 2 + r 2 − R 2 ) + R 2 cos − 1 ( 2 d R d 2 + R 2 − r 2 ) − 2 1 ( − d + r + R ) ( d + r − R ) ( d − r + R ) ( d + r + R ) where d is the distance between the centers of the two circles and R and r are the radii of the two circles.
In this case, R = 2 , r = 1 , and d = 2 2 and so the area A ≈ 0 . 1 0 8 .