Area Of A Quadrilateral!
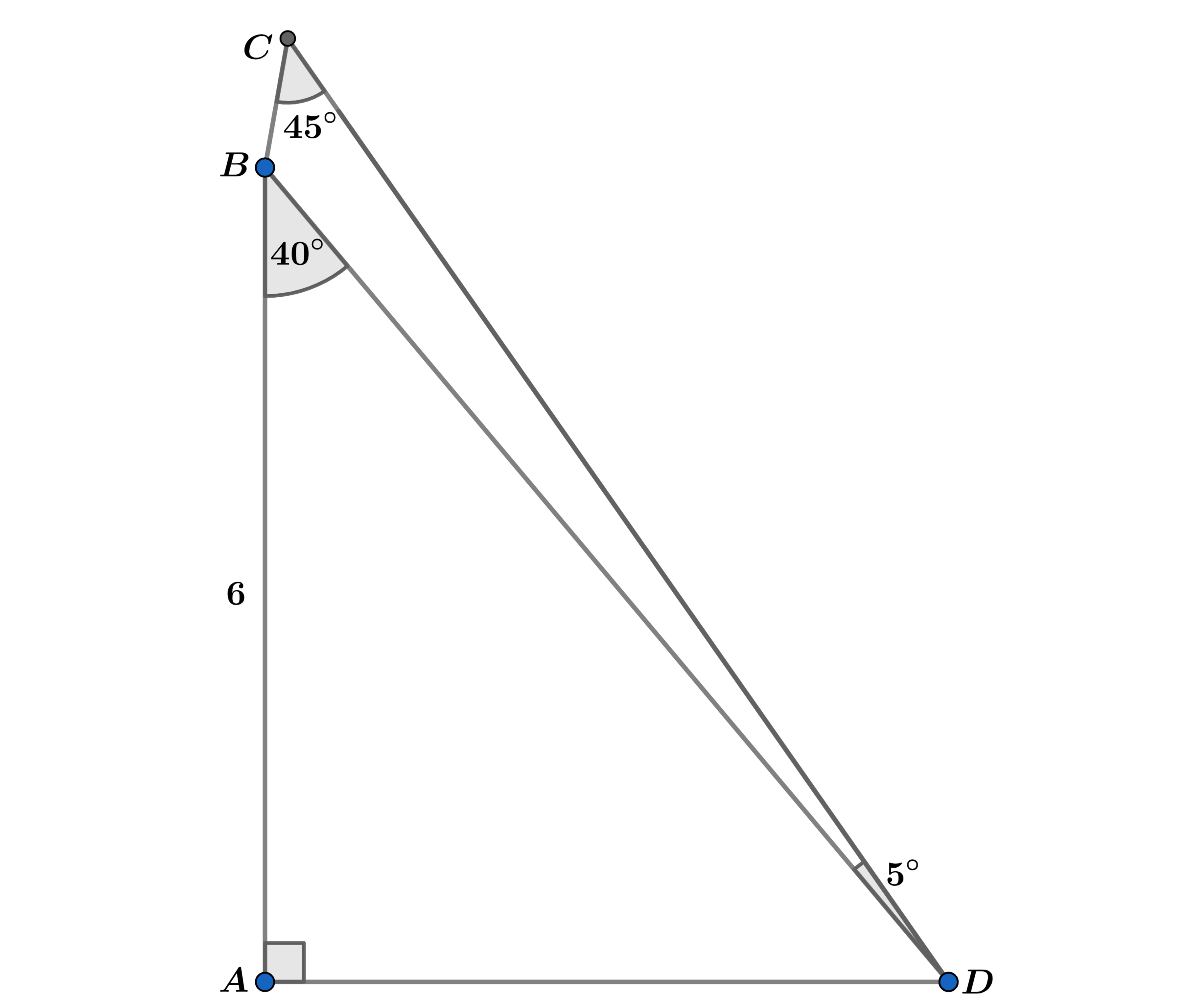
In the diagram above, ∠ A B D = 4 0 ∘ , ∠ B C D = 4 5 ∘ , ∠ B D C = 5 ∘
and A B = 6 .
Find the area of quadrilateral A B C D .
I found the above problem on YouTube, although my solution is different. Supposedly this problem was for 1 0 year old children in China.
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
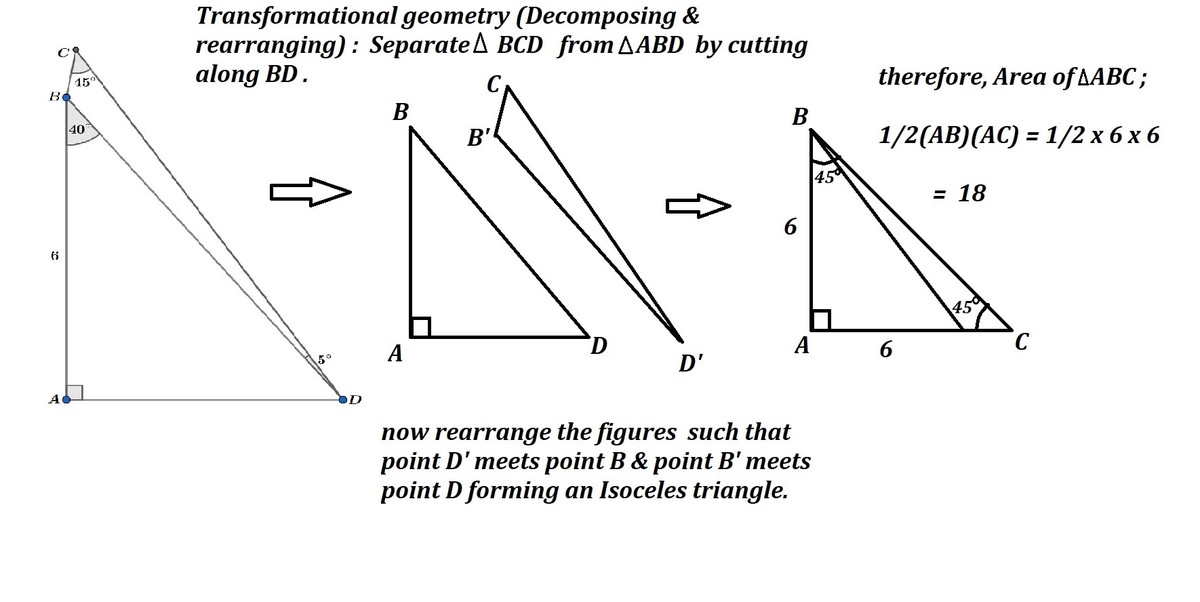
Very Nice Solution.
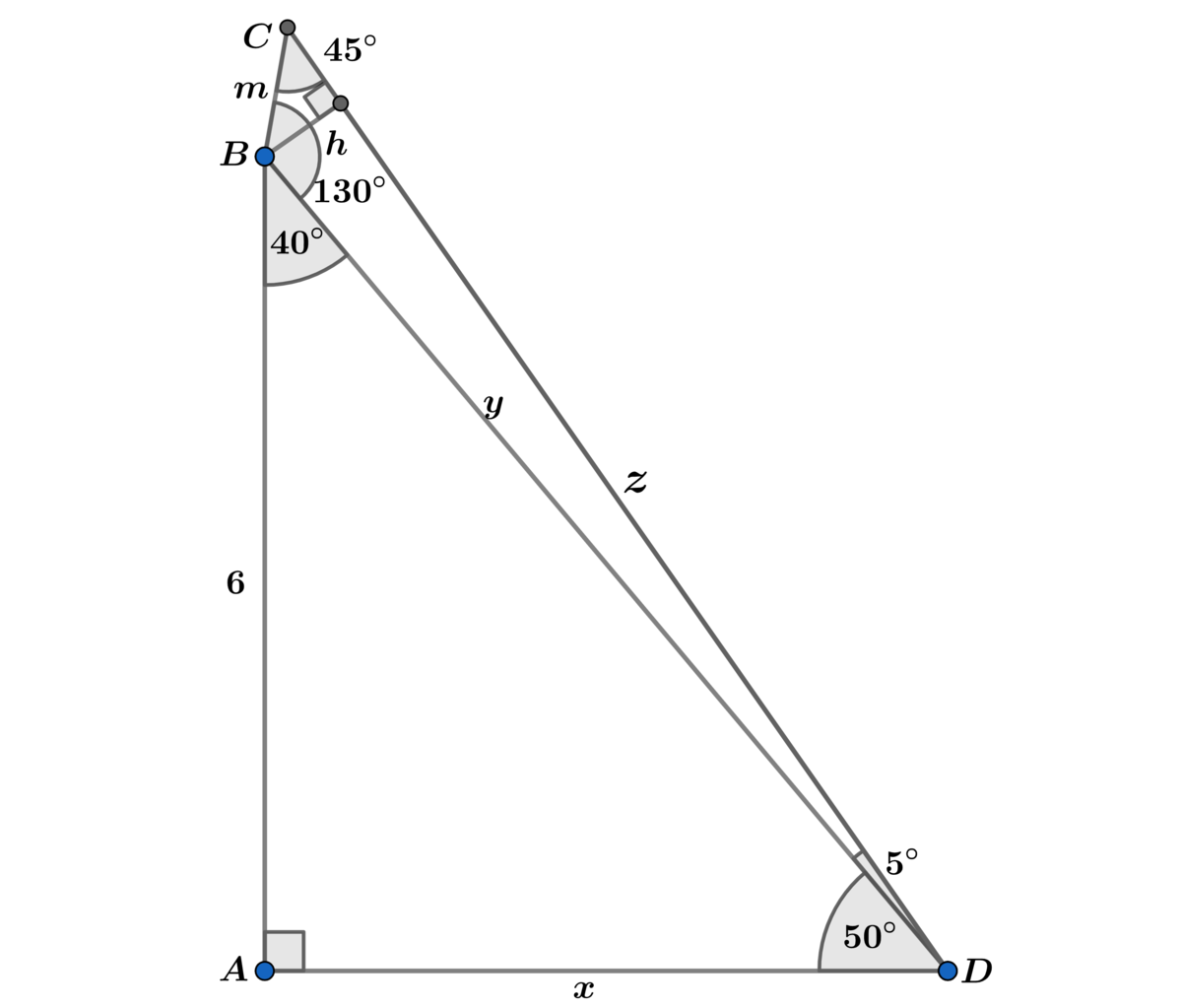
In right △ A B D we have:
x 6 = tan ( 5 0 ∘ ) ⟹ x = 6 cot ( 5 0 ∘ ) ⟹ y = 6 csc ( 5 0 ∘ )
Using the law of sines on △ B C D ⟹ sin ( 1 3 0 ∘ ) z = 6 2 csc ( 5 0 ∘ ) ⟹
z = 6 2 csc ( 5 0 ∘ ) sin ( 1 3 0 ∘ ) (will simplify all later)
and
sin ( 5 ∘ ) m = 6 2 csc ( 5 0 ∘ ) ⟹ m = 6 2 csc ( 5 0 ∘ ) sin ( 5 ∘ )
h = 2 m = 6 csc ( 5 0 ∘ ) sin ( 5 ∘ )
⟹ A △ A B D = 2 1 ( 6 ) ( 6 cot ( 5 0 ∘ ) ) = 1 8 cot ( 5 0 ∘ )
and
A B C D = 1 8 2 ( cot ( 5 0 ∘ ) sin ( 1 3 0 ∘ ) sin ( 5 ∘ )
⟹ A A B C D = 1 8 ( cot ( 5 0 ∘ ) + 2 csc 2 ( 5 0 ∘ ) sin ( 1 3 0 ∘ ) sin ( 5 ∘ ) )
and
cot ( 5 0 ∘ ) + 2 csc 2 ( 5 0 ∘ ) sin ( 1 3 0 ∘ ) sin ( 5 ∘ ) =
cot ( 5 0 ∘ ) + 2 csc 2 ( 5 0 ∘ ) sin ( 5 0 ∘ ) sin ( 5 ∘ ) =
sin ( 5 0 ∘ ) 1 ( cos ( 5 0 ∘ ) + 2 sin ( 5 ∘ ) ) =
sin ( 5 0 ∘ ) 1 ( cos ( 5 0 ∘ ) + 2 sin ( 4 5 ∘ − 4 0 ∘ ) ) =
sin ( 5 0 ∘ ) 1 ( cos ( 5 0 ∘ ) + cos ( 4 0 ∘ ) − sin ( 4 0 ∘ ) ) =
sin ( 5 0 ∘ ) 1 ( cos ( 5 0 ∘ ) + sin ( 5 0 ∘ ) − cos ( 5 0 ∘ ) ) = 1
⟹ A A B C D = 1 8 .
nice approach!