Area of a Quadrilateral!
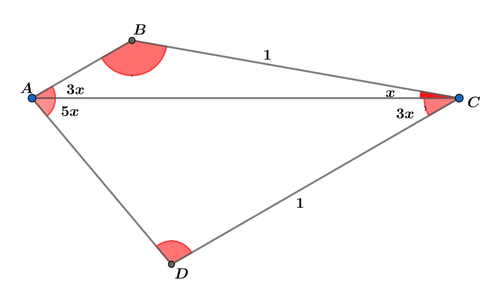
In quadrilateral A B C D above, ∠ B A C = 3 x , ∠ B C A = x , ∠ C A D = 5 x , ∠ A C D = 3 x and B C = C D = 1 . Find the area of quadrilateral A B C D .
Note: A variation of the above problem was taken from a problem I found online.
The answer is 0.43301270.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
... = 4 3
which is the area of an equilateral triangle with side 1 . I wonder if there's a direct geometric way to show that?
There is an excellent geometric proof of the fact that x = 1 0 ∘ by @Maria Kozlowska here .
From the angle conditions (solutions above showed that x = 1 0 ∘ ), we know that A B ∣ ∣ D C and so the quadrilateral is a trapezium, the height of the trapezium is 1 × sin ( 1 8 0 ∘ − ∠ A B C ) = sin 4 0 ∘ .
By sine rule, A B = sin 1 0 ∘ × sin 3 0 ∘ 1 = 2 sin 1 0 ∘ . So the area of quadrilateral A B C D is 2 1 ( 1 + 2 sin 1 0 ∘ ) ( sin 4 0 ∘ ) ≈ 0 . 4 3 3 0 1 2 7 0
By sine rule :
B C A C sin 3 x sin ( 1 8 0 ∘ − 4 x ) sin 3 x sin 4 x sin 3 x 1 sin 3 x sin 5 x sin 3 x sin 5 x ⟹ 5 x ⟹ 3 x = C D A C = 1 A C = sin 5 x sin ( 1 8 0 ∘ − 8 x ) = sin 5 x sin 8 x = sin 5 x 2 cos 4 x = 2 cos 4 x = 2 1 sin ( 9 0 ∘ − 4 x ) = 9 0 ∘ − 4 x ⟹ x = 1 0 ∘ = 3 0 ∘ ⟹ x = 1 0 ∘ SInce sin ( 1 8 0 ∘ − θ ) = sin θ And sin 2 θ = 2 sin θ cos θ Also sin θ = cos ( 9 0 ∘ − θ )
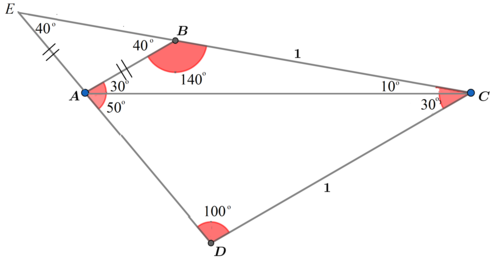
Fill in the measures of all the angles. Extend B C and D A to meet at E . Then we note that ∠ E = 4 0 ∘ and △ C D E and △ A B E are isosceles and similar. Therefore the area of quadrilateral A B C D :
[ A B C D ] = [ C D E ] − [ A B E ] = 2 1 ⋅ 1 2 ⋅ sin 8 0 ∘ − 2 1 ⋅ A B 2 ⋅ sin 8 0 ∘ = 2 sin 8 0 ∘ ( 1 − sin 2 3 0 ∘ sin 2 1 0 ∘ ) ≈ 0 . 4 3 3 By sine rule, A B = sin 3 0 ∘ sin 1 0 ∘
For △ A D C :
D C sin ( 5 x ) = A C sin ( 8 x ) ⟹ sin ( 8 x ) sin ( 5 x ) = A C D C = A C B C = A C 1
For △ A B C :
B C sin ( 3 x ) = A C sin ( 4 x ) ⟹ sin ( 4 x ) sin ( 3 x ) = A C B C = = A C 1
⟹
sin ( 8 x ) sin ( 5 x ) = sin ( 4 x ) sin ( 3 x ) ⟹ sin ( 5 x ) sin ( 4 x ) = sin ( 8 x ) sin ( 3 x ) =
2 sin ( 4 x ) cos ( 4 x ) sin ( 3 x ) ⟹ sin ( 5 x ) = 2 cos ( 4 x ) sin ( 3 x )
Using the identity 2 cos ( A ) sin ( B ) = sin ( A + B ) − sin ( A − B ) , with A = 4 x and
B = 3 x we obtain: sin ( 5 x ) = sin ( 7 x ) − sin ( x ) ⟹ sin ( 7 x ) − sin ( 5 x ) = sin ( x )
or sin ( 7 x ) + sin ( − 5 x ) = sin ( x )
Using the identity sin ( A ) + sin ( B ) = 2 sin ( 2 A + B ) cos ( 2 A − B ) , with A = 7 x and
B = − 5 x we obtain: 2 sin ( x ) cos ( 6 x ) = sin ( x ) ⟹ 2 cos ( 6 x ) = 1 ⟹ cos ( 6 x ) = 2 1
⟹ 6 x = 6 0 ∘ ⟹ x = 1 0 ∘
Using the above diagram with x = 1 0 ∘ ⟹ h 2 = sin ( 3 0 ∘ ) = 2 1 and h 1 = sin ( 1 0 ∘ )
For A C we have: sin ( 1 4 0 ∘ ) A C = sin ( 3 0 ∘ ) 1 = 2 ⟹ A C = 2 sin ( 1 4 0 ∘ )
⟹ The total area A A B C D = 2 1 ( 2 sin ( 1 4 0 ∘ ) sin ( 1 0 ∘ ) ) + 2 1 ( 2 sin ( 1 4 0 ∘ ) ) ( 2 1 ) =
sin ( 1 4 0 ∘ ) ( sin ( 1 0 ∘ ) + 2 1 ) = 2 1 sin ( 1 4 0 ∘ ) ( 2 sin ( 1 0 ∘ ) + 1 ) ≈ 0 . 4 3 3 0 1 2 7 0