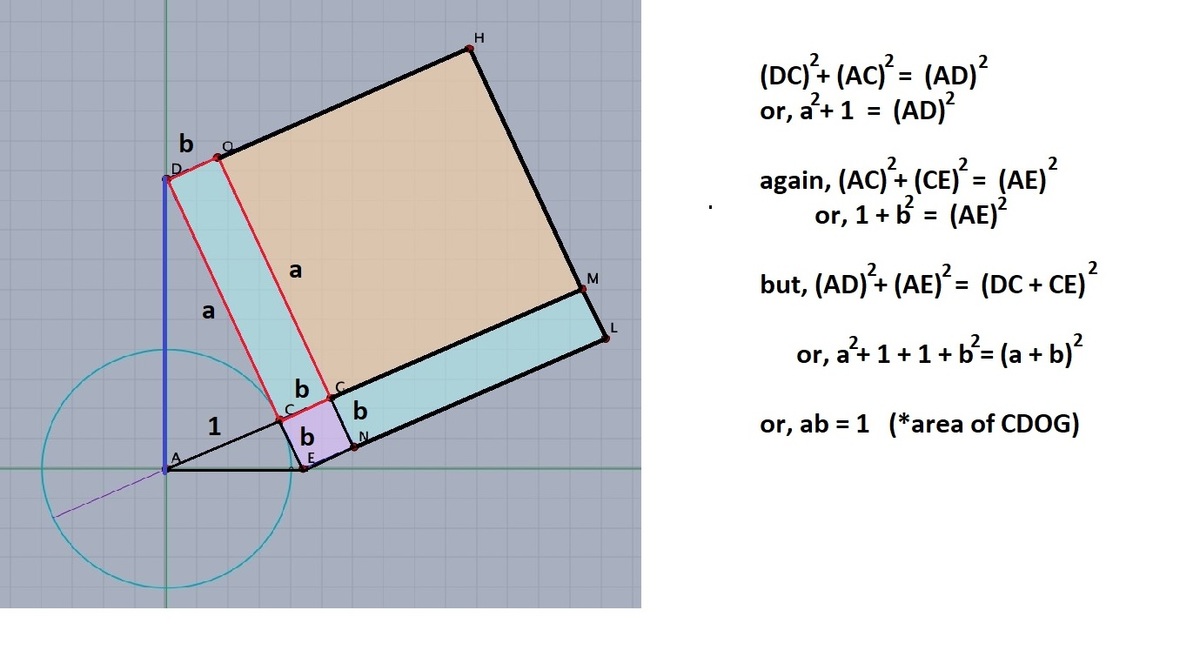
Area of a quadrilateral CGOD

Geometry Level 3

In the above diagram.

Given the unit circle with a center at A and the segment ED tangent at the point C.

What is the area of the quadrilateral CDOG.


The answer is 1.

Emir Fassad by Emir Fassad , 88, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Nibedan Mukherjee
May 30, 2019

1 Helpful 1 Interesting 1 Brilliant 0 Confused
Emir Fassad
May 28, 2019

The segment EC is equal to the tangent of the angle EAC. Likewise the segment CD is equal to the cotangent of that angle. The area of the rectangle ELHD is thus: ( tan ⁡ + cot ⁡ ) 2 = tan ⁡ 2 + 2 × tan ⁡ cot ⁡ + cot ⁡ 2 = tan ⁡ 2 + cot ⁡ 2 + 2 sin ⁡ cos ⁡ cos ⁡ sin ⁡ = tan ⁡ 2 + cot ⁡ 2 + 2 (\tan + \cot )^{2} = \tan ^{2} + 2 \times \tan \cot + \cot ^{2} = \tan ^{2} + \cot ^{2} + 2 \frac {\sin}{\cos} \frac {\cos}{\sin} =\tan ^{2} + \cot ^{2} +2

The rectangles CDOG and NLMG are each equal to the product of the tangent and cotangent of the angle EAC. Hence each of them has the value one.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Can you Show this construction leads to a unique solution? Or at least solutions with equal area?

Edit: I missread an thought youre looking for the area of the big square.

Eric Scholz - 2 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...