Area Of Quadrilateral Given All Its Sides?
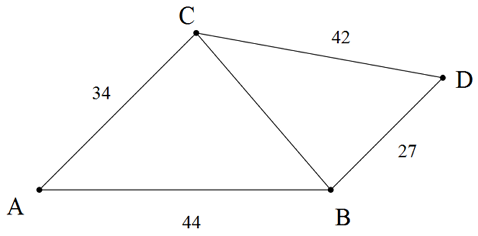
Consider a quadrilateral
with sides
and
.
Find the area of the quadrilateral
.
Give your answer to 2 decimal places.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider △ C A B . We have the lengths of two of its sides, but there are infinity triangles with this 2 sides, so there are infinity possible areas for this triangle (with some restrictions).
Now, consider △ C D B . For each of the △ C A B possible areas, C B has a different length; thus, there exists a △ C D B for each △ C A B . As ( A B C D ) = ( △ C A B ) + ( △ C D B ) , there are infinity possible values for the area of the quadrilateral. ( ( △ C A B ) denotes the area of △ C A B )
Note that the reasoning is based on the Congruence Theorem SSS, which states that 3 sides determine one single triangle, but 2 sides determine infinity triangles. We need, at least, another segment length or a quadrilateral angle.
For example:
If ( △ C A B ) = 7 0 4 , as one of the ( △ C A B ) bases is A B , then 7 0 4 = 2 A B ⋅ h A B .
Thus, h A B = 3 2 . As sin ( ∡ A ) = A C h A B , therefore, ∡ A ≈ 7 0 . 2 5 ° . Applying Law of Cosines:
C B 2 = A B 2 + A C 2 + 2 ⋅ A C ⋅ A B ⋅ cos ∡ A . Replacing the known values and solving, A C ≈ 6 4 .