Area of a Rose of 2021 Petals.

We are going to solve this problem in a more general context. Assume that in the definition of $R$ we replace 2021 by a number of the form $2n-1,$ where $n>2$ and $2n-1$ is not a multiple of 3. Then the region $R$ is going to be the region bounded by the rose defined by $r=\cos {(\frac{2n-1}{3}\theta)}.$ Under the assumptions made before that $2n-1$ must be an odd number greater than or equal to 5 and not a multiple of 3, the rose will have $2n-1$ identical petals. Additionally, the whole curve is traced when $-\frac{3\pi}{2}\leq \theta \leq -\frac{3\pi}{2} ,$ and two contiguous petals overlap.

For example, we include below the graph of $r=\cos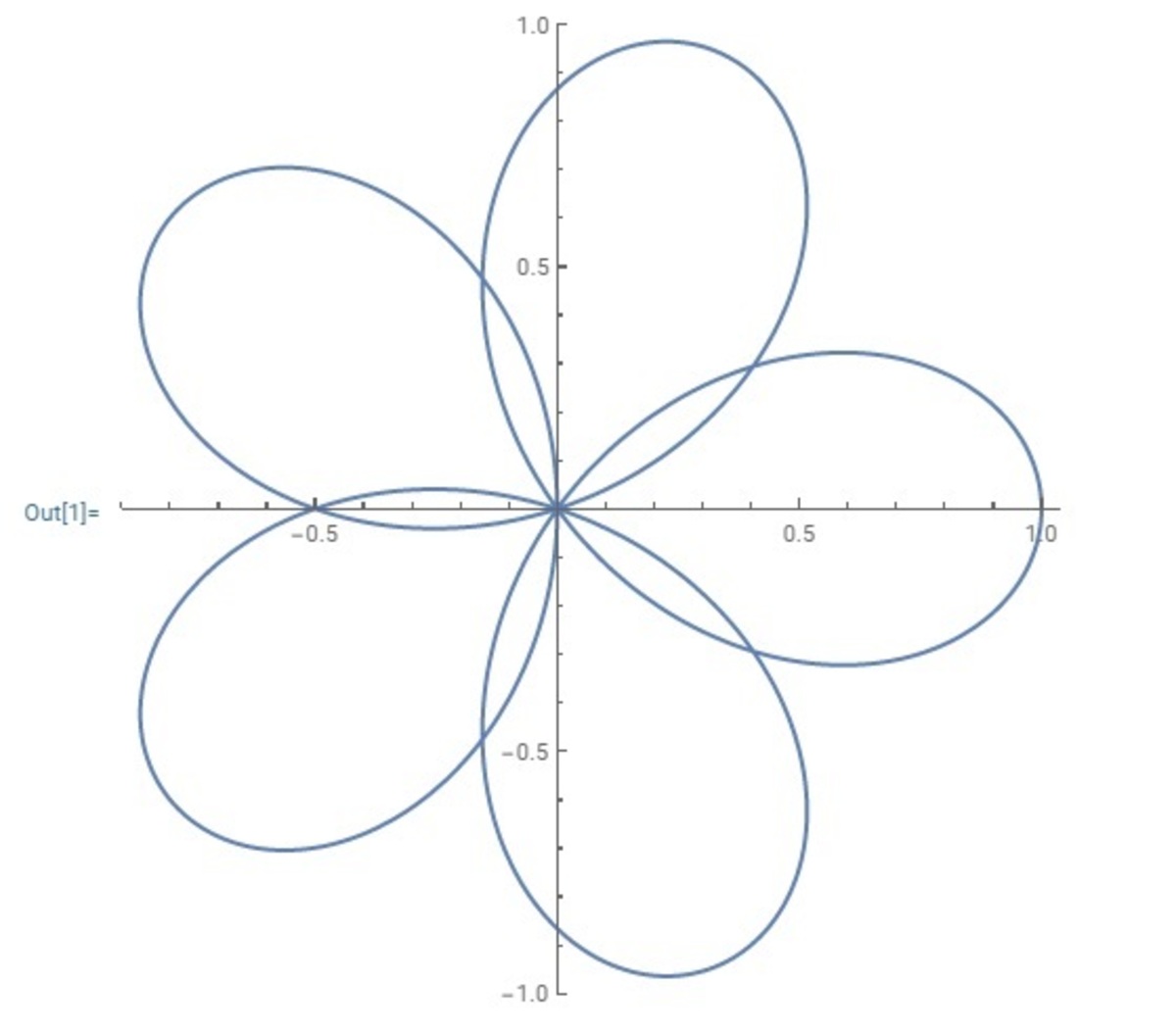{\frac{5}{3}\theta}$ To avoid overlapping, we can consider the whole region enclosed by the rose as the union of $2n-1$ non-overlapping subregions of the form given by the following picture

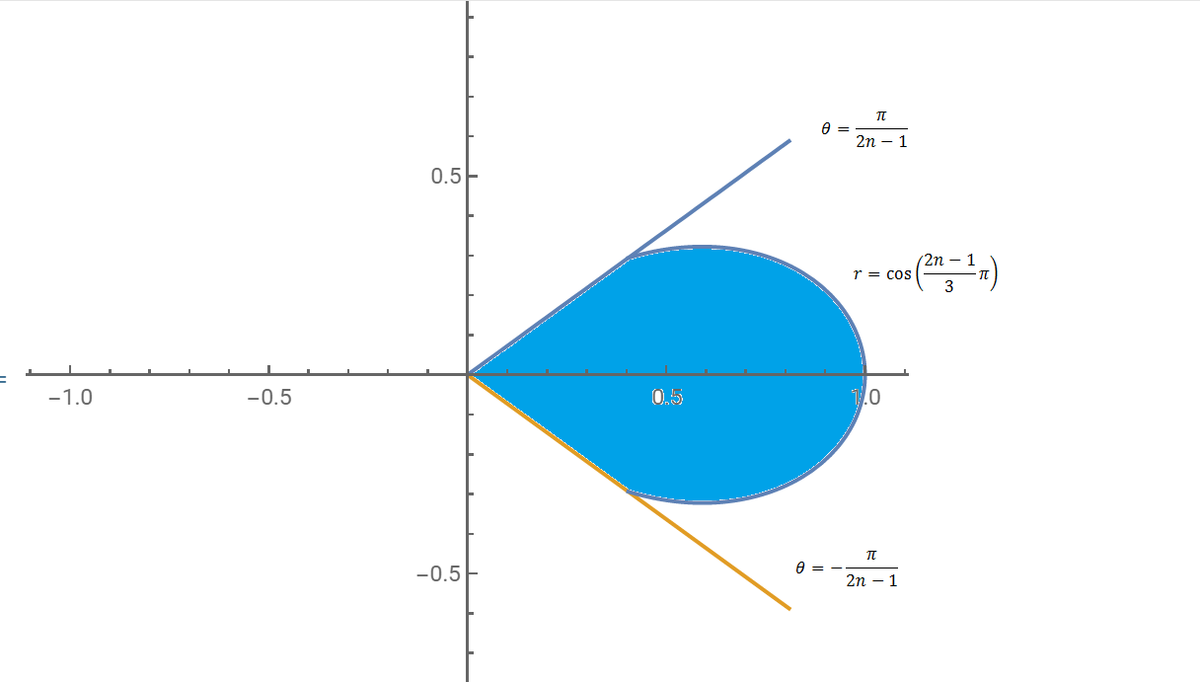
Then the area of the region $R$ enclosed by the rose is $A=(2n-1) *\frac{1}{2} \int_{-\frac{\pi}{2n-1}}^{\frac{\pi}{2n-1}} \cos^2{\left (\frac{2n-1}{3}\theta \right )} \, d\theta=\frac{ 3\sqrt{3}}{8}+\frac{\pi}{2}.$ The result that we have obtained does not depend on $n,$ therefore, this will be the area of $R$ in the case that $2n-1=2021.$ Then the answer is $\boxed{2.22}.$