Area Of A Shaded Region.

Since $ABDC$ is a cyclic quadrilateral , $\angle ADC = \angle ABC = 30^\circ$ and $\angle CAD = \angle CBD = 30^\circ$ , therefore $\triangle ACD$ is isosceles and $AC=CD=a$ . Also the angle at the center is twice at at the circumference, then $\angle APD = 2\angle ABC = 120^\circ$ , therefore $\triangle APD$ is an isosceles triangle congruent to $\triangle ACD$ , implying that the radius of the circle is $a$ .

To find $a$ , we note that $AD = 2a\cos 30^\circ = \sqrt 3 a$ . By cosine rule ,

$\begin{aligned} (\sqrt 3a)^2 & = 10^2 + 12^2 - 2(10)(12)\cos 60^\circ \\ 3a^2 & = 124 \\ \implies a & = 2\sqrt{\frac {31}3} \end{aligned}$

Area of the shaded region is given by:

$\begin{aligned} A & = A_{\bigcirc} - A_{\triangle ABD} - A_{\triangle ACD} \\ & = \pi a^2 - \frac 12 (10)(12)\sin 60^\circ - \frac 12 a^2 \sin 120^\circ \\ & = \frac {124}3 \pi - 30\sqrt 3 - \frac {31\sqrt 3}3 \\ & = \frac {124}3 \pi - \frac {121}{\sqrt 3} \end{aligned}$

Therefore $a+b+c = 124+3+121 = \boxed{248}$ .

Let the radius of the circle be $r$ and the angle $\angle {PBC}$ be $α$ . Then

$2r\cos (30\degree+α)=10\implies r(\sqrt 3\cos α-\sin α)=10$

$2r\cos (30\degree-α)=12\implies r(\sqrt 3\cos α+\sin α)=12$

From these we get $r^2=\dfrac{124}{3}, \tan α=\dfrac{\sqrt 3}{11}$ .

Hence $\tan (30\degree-α)=\dfrac{2}{3\sqrt 3}$ and $\tan (30\degree+α)=\dfrac{7}{5\sqrt 3}$ .

Total area of bottom two regions is $2\times (\dfrac{πr^2}{6}-\dfrac{\sqrt 3r^2}{4})=\dfrac{πr^2}{3}-\dfrac{\sqrt 3r^2}{2}=\dfrac{πr^2}{3}-\dfrac{62}{\sqrt 3}$ .

Area of top left region is $\dfrac{r^2(\dfrac{2π}{3}-2α)}{2}-25\tan (30\degree+α)$ .

Area of top right region is $\dfrac{r^2(\dfrac{2π}{3}+2α)}{2}-36\tan (30\degree-α)$ .

Sum of these two is $\dfrac{2πr^2}{3}-\dfrac{59}{\sqrt 3}$ .

Therefore the total area is $πr^2-\dfrac{121}{\sqrt 3}=\dfrac{124π}{3}-\dfrac{121}{\sqrt 3}$ .

So $a=124,b=3, c=121$ and $a+b+c=\boxed {248}$ .

$m\angle{ABC} = 30^{\circ} = m\angle{CBD} \implies m(\stackrel\frown{AC}) = 60^{\circ} = m(\stackrel\frown{CD}) \implies$ $\overline{AC} \cong \overline{CD}$ .

$\implies 100 + x^2 - 10\sqrt{3}x = 144 + x^2 - 12\sqrt{3}x \implies 2\sqrt{3}x = 44 \implies x = \dfrac{22}{\sqrt{3}}$ .

$h_{1} = 10\sin(30^{\circ}) = 5$ and $h_{2} = 12\sin(30^{\circ}) = 6 \implies$ $A_{1} = \dfrac{1}{2}(\dfrac{22}{\sqrt{3}})(5) = \dfrac{55}{\sqrt{3}}$ and

$A_{2} = \dfrac{66}{\sqrt{3}} \implies A_{T} = A_{1} + A_{2} = \dfrac{121}{\sqrt{3}}$ .

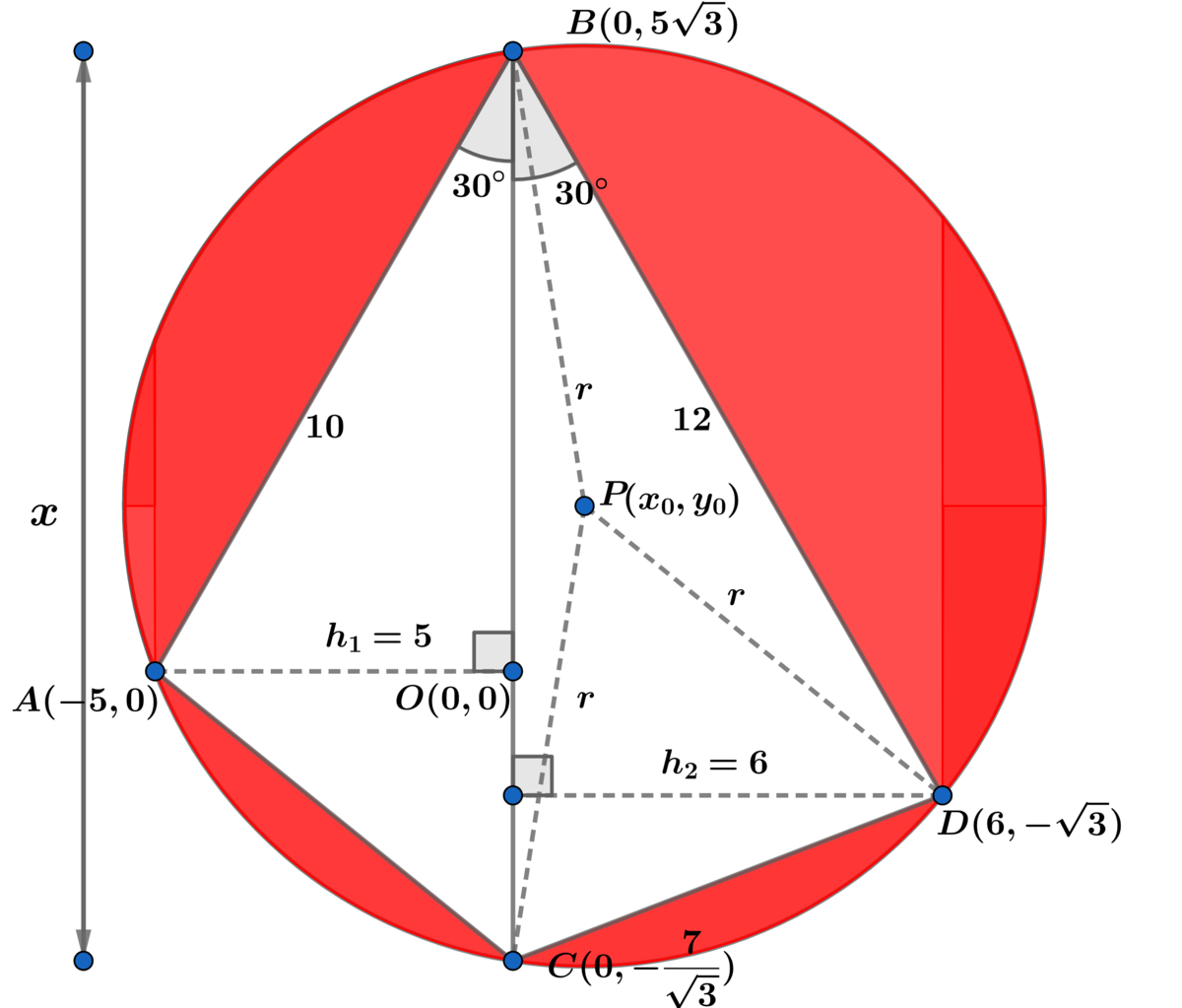
Assigning coordinates we have:

$r^2 = x_{0}^2 + (y_{0} - 5\sqrt{3})^2$

$r^2 = x_{0}^2 + (y_{0} + \dfrac{7}{\sqrt{3}})^2$

$\implies$ $\dfrac{44}{\sqrt{3}}y_{0} = \dfrac{176}{3} \implies y_{0} = \dfrac{4}{\sqrt{3}}$

and

$r^2 = (x_{0} - 6)^2 + (y_{0} + \sqrt{3})^2$

$r^2 = x_{0}^2 + (y_{0} + \dfrac{7}{\sqrt{3}})^2$

using $y_{0} = \dfrac{4}{\sqrt{3}} \implies$

$x_{0}^2 - 12x_{0} + 36 + \dfrac{49}{3} = r^2$

$x_{0}^2 + \dfrac{121}{3} = r^2$

$\implies -12x_{0} + 12 = 0 \implies x_{0} = 1 \implies P(1,\dfrac{4}{\sqrt{3}}) \implies r^2 = \dfrac{121}{3} + 1 =$ $\dfrac{124}{3}$

$\implies r = 2\sqrt{\dfrac{31}{3}} \implies$ Area of the circle $A_{c} = \dfrac{124}{3}\pi$ and $A_{T} = \dfrac{121}{\sqrt{3}} \implies$

The desired shaded area $A = A_{c} - A_{T} = \dfrac{124}{3}\pi - \dfrac{121}{\sqrt{3}} =$ $\dfrac{a}{b}\pi - \dfrac{c}{\sqrt{b}} \implies$

$a + b + c = \boxed{248}$