Area of a star inside a unit square
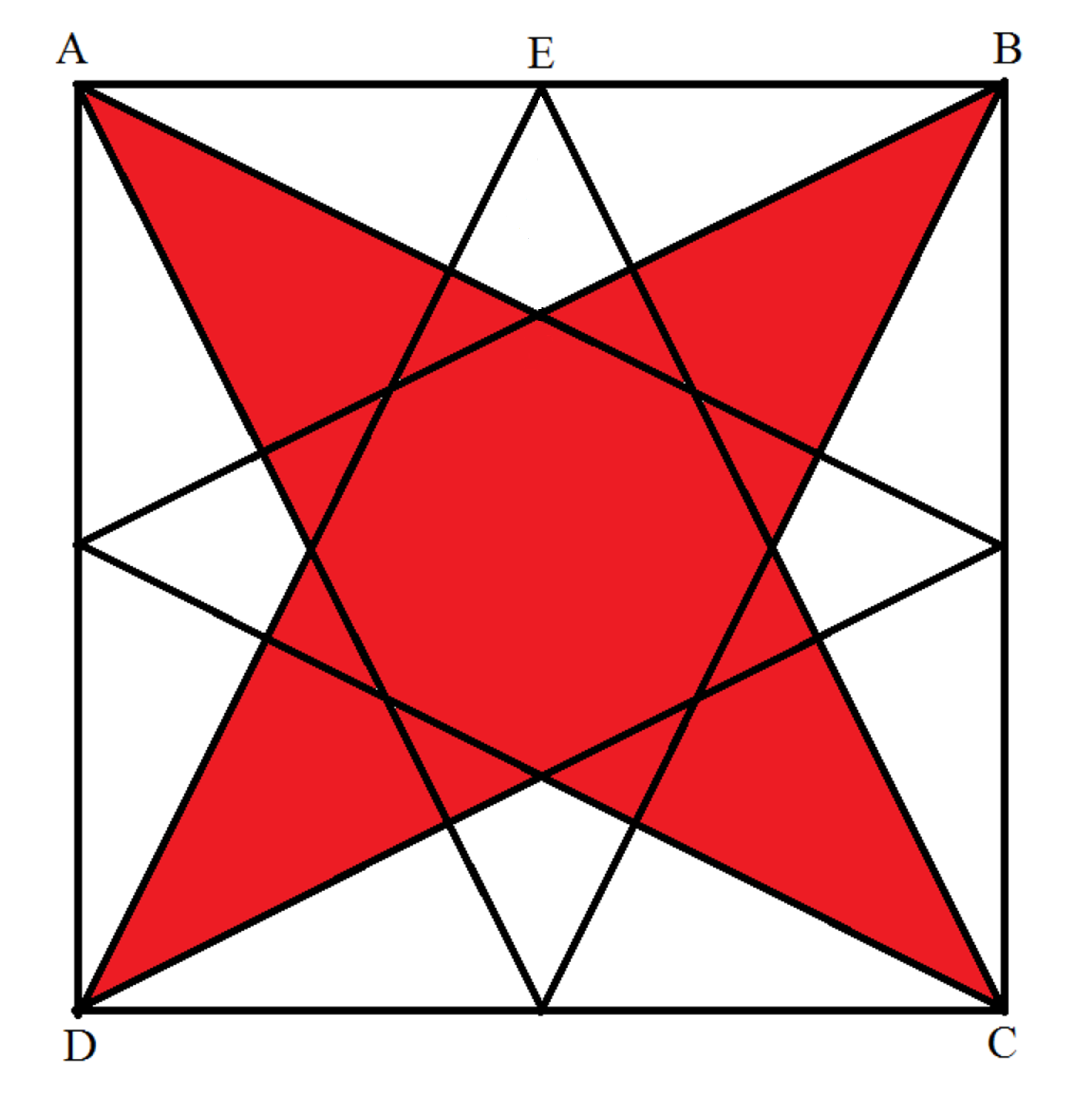
Find the area of a star colored in red inscribed in a unit square according to the picture below.
∣
A
E
∣
=
2
1
and other edges follow the same pattern.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice. I used your image since it looks much cleaner. Hope you don't mind. :)
Area of each white triangle is 2 1 × 1 × 4 1 = 8 1 . So total area of the four white triangles is 4 × 8 1 = 2 1 . Therefore area of the red region is 1 − 2 1 = 2 1 .
To find the area of the red section, you must determine the area of the white triangles combined, subtract this from the total area of the square.
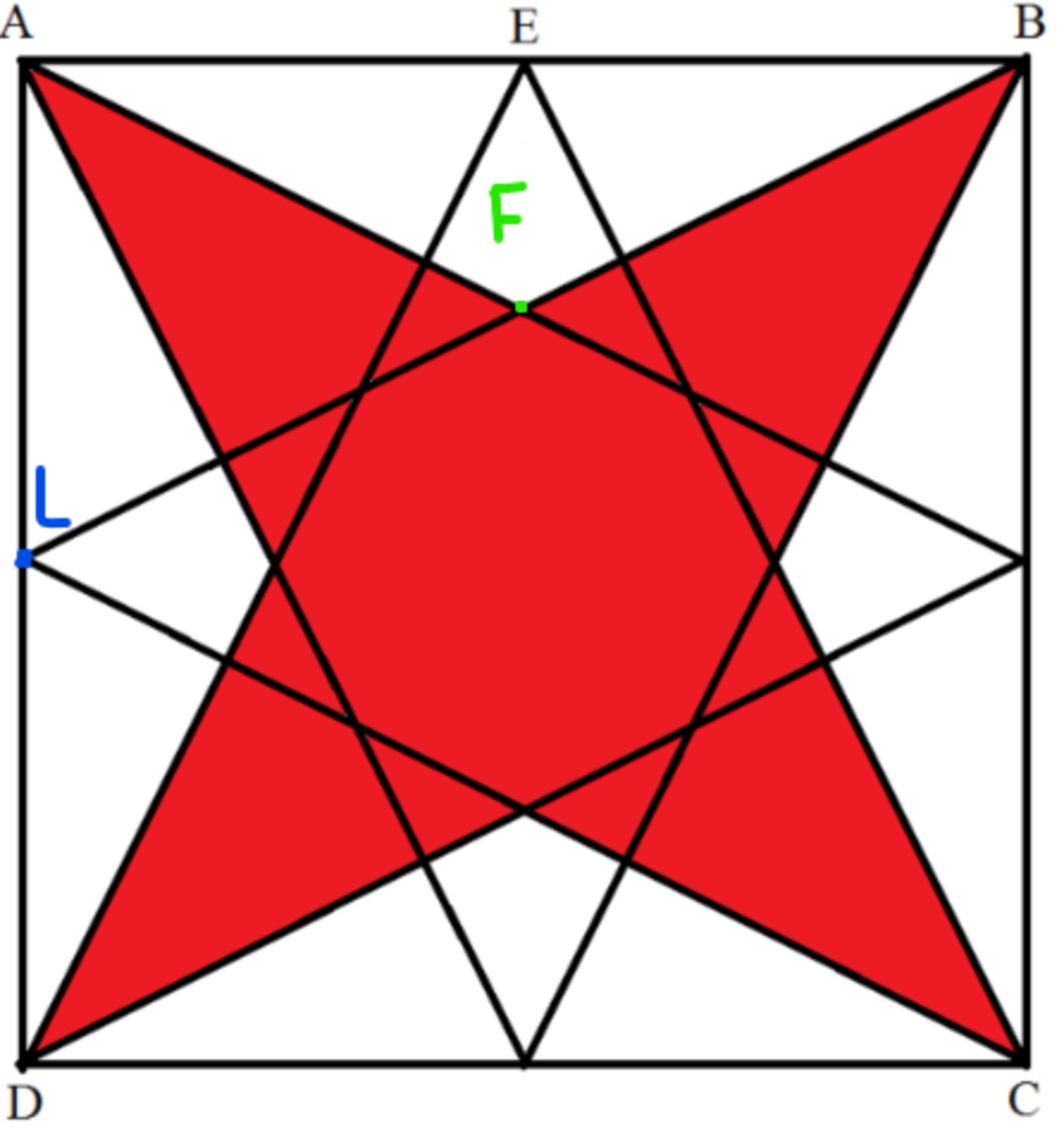
A E = 2 1 , meaning that A B = 1. A L = 2 1 , meaning that E F = 2 1 of A L , or 4 1 .
We now have A B and E F , meaning that we know the b a s e and h e i g h t of the top white triangle. The formula for the area of a triangle is 2 b a s e ∗ h e i g h t , so the area of the white triangle would be ( 4 1 x 1) ÷ 2 = 8 1 . All of the white triangles are congruent, and there are 4 of them, meaning 8 1 x 4 = 2 1 = the total white triangle area.
The total area of the square (1 x 1 = 1) minus the combined area of the white triangles = 1 - 2 1 = 2 1 = the area of the red figure.
Label the figure as above. We note that △ C B E and △ B E F are similar. Therefore B E E F = B C B E ⟹ E F = B C B E × = 1 2 1 × 2 1 = 4 1 .
Then the area of △ B E F , A △ B E F = 2 1 × 2 1 × 4 1 = 1 6 1 . The area of white region A white = 8 A △ B E F = 8 × 1 6 1 = 2 1 . The area of the red region A red = A square − A white = 1 − 2 1 = 2 1 .