area of a triangle - 2
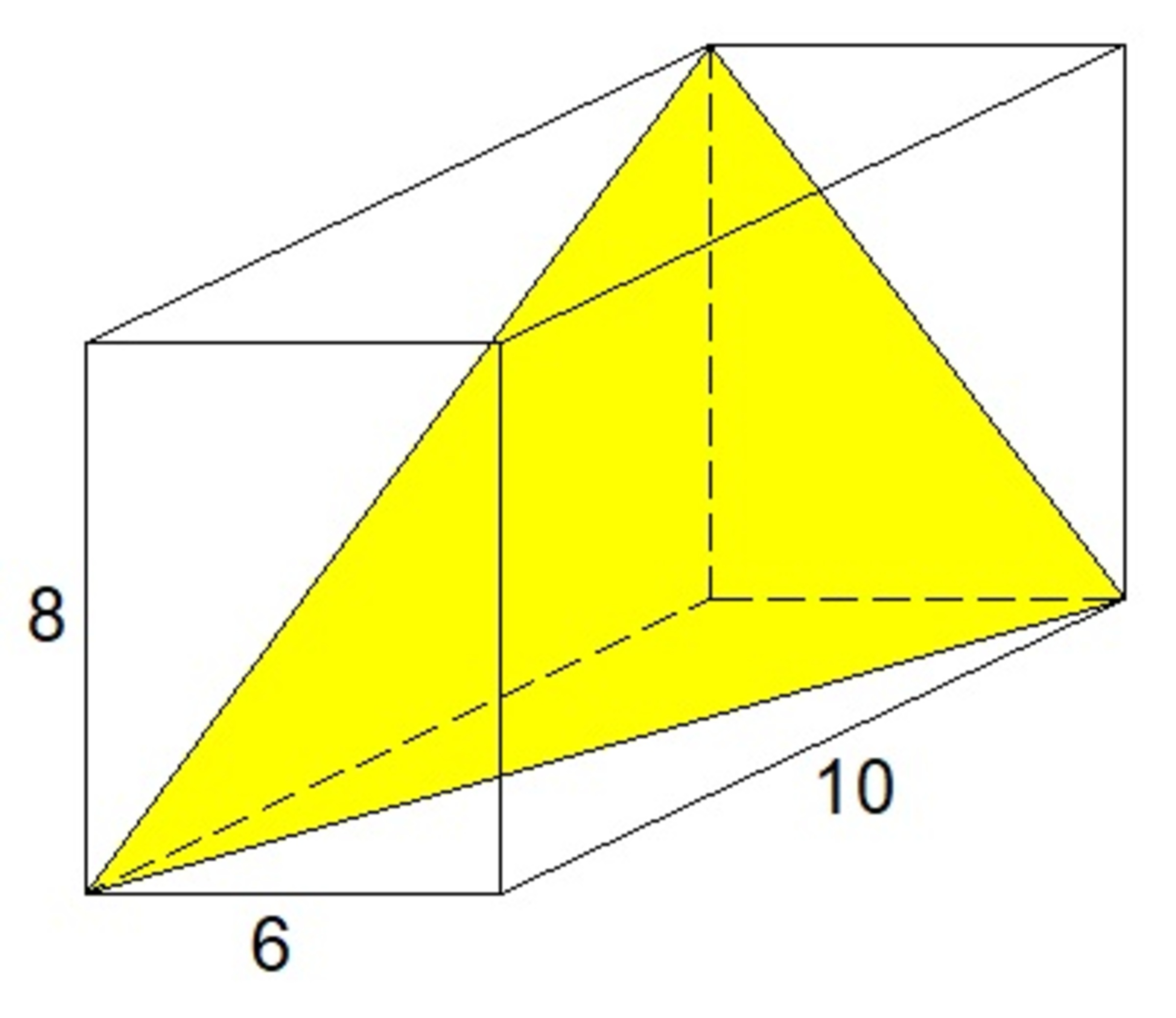 Three vertices of a cuboid are joined to form a triangle as shown. Find the area of this triangle. If your answer can be expressed as
where
and
are positive co-prime integers and
is square free, submit
.
Three vertices of a cuboid are joined to form a triangle as shown. Find the area of this triangle. If your answer can be expressed as
where
and
are positive co-prime integers and
is square free, submit
.
The answer is 771.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the vertices of the triangle be ( 1 0 , 0 , 0 ) , ( 0 , 6 , 0 ) and ( 0 , 0 , 8 ) . Then the area of the triangle is 2 1 ∣ ( 1 0 i − 6 j ) × ( 8 k − 6 j ) ∣ , where i , j , k are the unit vectors along the X , Y and Z -axes respectively. Carrying out the vector product and extracting the magnitude we get the area equal to 2 1 1 2 3 0 4 = 2 7 6 9 . Hence a = 2 , b = 7 6 9 and a + b = 7 7 1