Area of ABC?
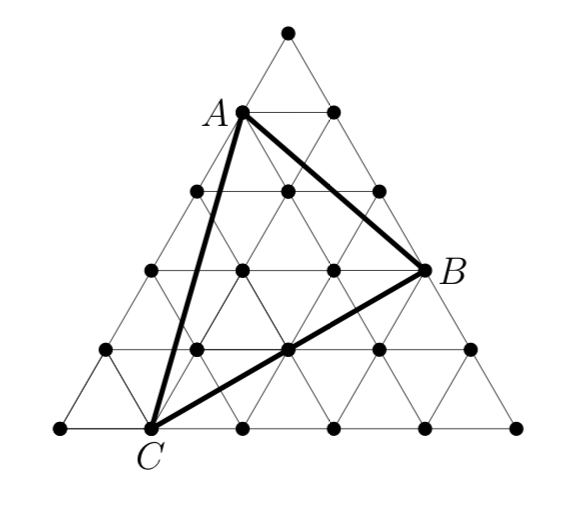 The figure consists of 25 equilateral triangles, each of area 1
. What is the area of
The figure consists of 25 equilateral triangles, each of area 1
. What is the area of
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.



The whole diagram can be sheared to a rectangular grid while preserving area:
The triangle goes through B = 4 boundary points and has I = 4 interior points. If the rectangles were unit squares, then by Pick's Theorem the area would be A = I + 2 1 B − 1 = 4 + 2 1 ⋅ 4 − 1 = 5 .
However, since each rectangle is made up of 2 unit triangles for an area of 2 instead of 1 , the area is doubled, and so A = 2 I + B − 2 = 2 ⋅ 4 + 4 − 2 = 1 0 .