Area of an n -gon on the Complex Plane
When the roots of x 9 + x 8 + x 7 + x 6 + x 5 + x 4 + x 3 + x 2 + x + 1 and 1 are simultaneously graphed on the complex plane, a regular n -gon is formed with area q . Find n + q rounded to the nearest integer.
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yup!! Did it the same way!!
Perfect!
can you please express that little trigonometry
Log in to reply
The radius of the 10-sided regular polygon is 1 . Divide it into 10 triangles and you'll notice that they are isosceles, and name the different side L . Take one triangle and bisect it by the different angle. Let's call the angle bisector a . Now, you'll get a right triangle with sides a , 2 L and hypotenuse 1 . But, the angle opposite to 2 L is 1 0 π . So, by the sine function, we get L = 2 sin ( 5 π ) and by the cosine function a = cos ( 5 π ) . With the formula of the area of a polygon: A = 2 a L n , substitute: A = 2 cos ( 5 π ) ( 2 sin ( 5 π ) ) ( 1 0 ) , use a trigonometric identity to get: A = 5 sin ( 5 π )
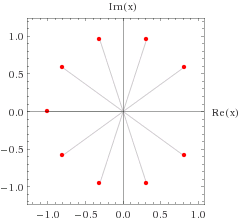
The above graph plots the complex roots of given equation, and by adding plot of 1+0i, i.e. (1,0) in the complex plane in the above graph, we get a regular polygon of 10 sides, and we can approximate it's area to the area of unit circle. Thus, the answer is :- n+q=floor(10+3.14....)=13.
If we multiply that equation by ( x − 1 ) , we obtain x 1 0 − 1 , which also contains the point ( 1 , 0 ) . Now, that equation represents the 10th roots of unity, and we know if that is plotted, there will be a regular polygon of 10 sides, so n = 1 0 . And the area of that polygon, after a little trigonometry, will be q = 5 sin ( 5 π ) . So, p + q ≈ 1 2 . 9 3 , and rounded to the nearest integer, 1 3 .