Area of Annulus
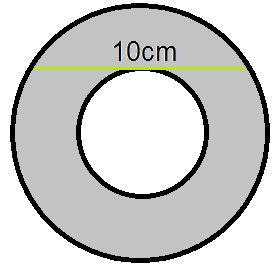 The area of the annulus (the shaded region) can be expressed in the form of aπ cm², where a is an integer. What is the value of a?
The area of the annulus (the shaded region) can be expressed in the form of aπ cm², where a is an integer. What is the value of a?
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
[The diagram] (https://lh4.googleusercontent.com/-aTLIl2paZDk/U7jlAtAFTkI/AAAAAAAABBY/AA-Vd4nBxcY/w426-h412/Brilliant01.png)
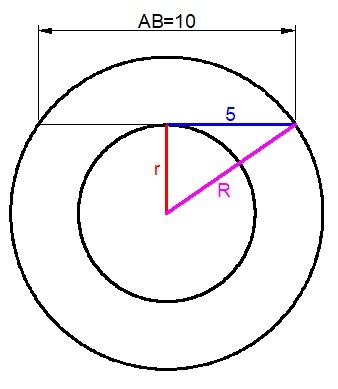
The area between the two circles is
A = π R 2 − π r 2 = π ( R 2 − r 2 )
Using pythagorean theorem, we have
R 2 = r 2 + 5 2
R 2 − r 2 = 2 5
Finally,
A = π ( 2 5 )
So the desired answer is 2 5 .
Let the outer circle have radius R and the inner circle radius r. Then we can form a right triangle using these two radii and one-half of the 10 cm chord. We then have
R 2 = r 2 + 5 2 , which can be rewritten as R 2 - r 2 = 25.
But the area of the annulus is just p i * [ R 2 - r 2 ], so the value of a is 2 5 .
This is an interesting question. Now we know that we can find the area of an annulus with only one measurement. I thought we need to know the internal and external radii.
Back to the question. The area of the annulus A = π ( R 2 − r 2 ) , where R and r are the external and internal radii of the annulus respectively. Since A = a π cm 2 , then a = R 2 − r 2 .
Let the 1 0 -cm line meets the external circle at A and B and touch the internal circle at M , and center of the annulus be O . We note that A O = B O = R and M O = r . We also note that A O 2 − M O 2 = A M 2 . And since A M = B M = 5 cm, we have R 2 − r 2 = 5 2 or a = 2 5 .