Area of Center Locus
An ellipse with semi-major axis and semi-minor axis is sliding in place, such that it is always tangent to the x-axis at the origin, as shown in the animation image below. The center of the ellipse traces a closed locus. Find the area enclosed by this locus in terms of and .
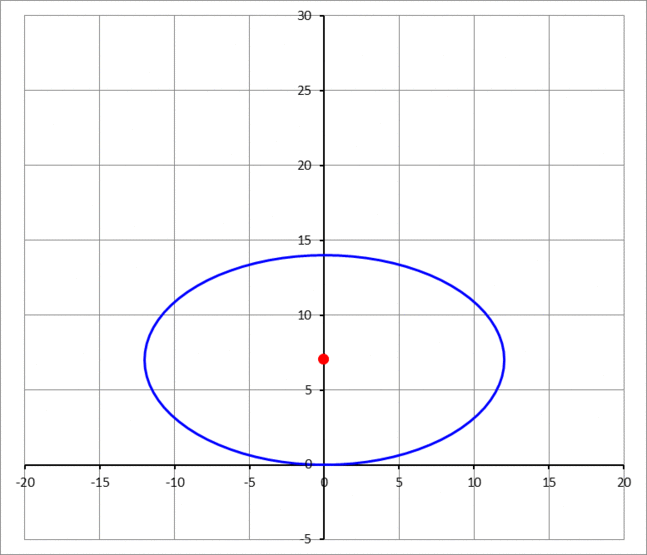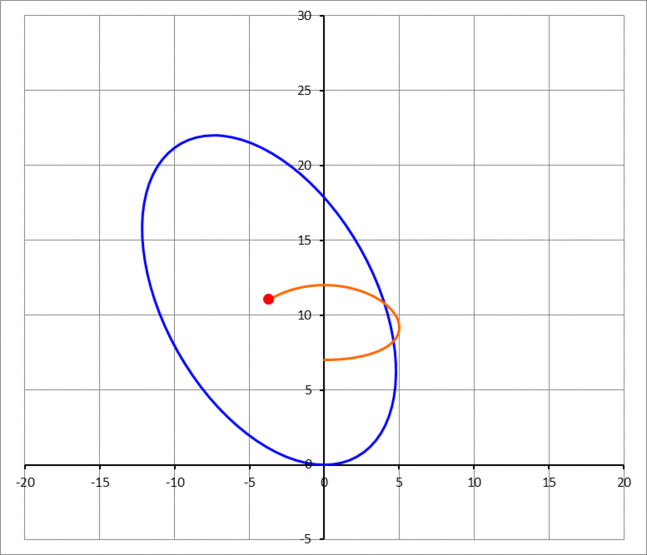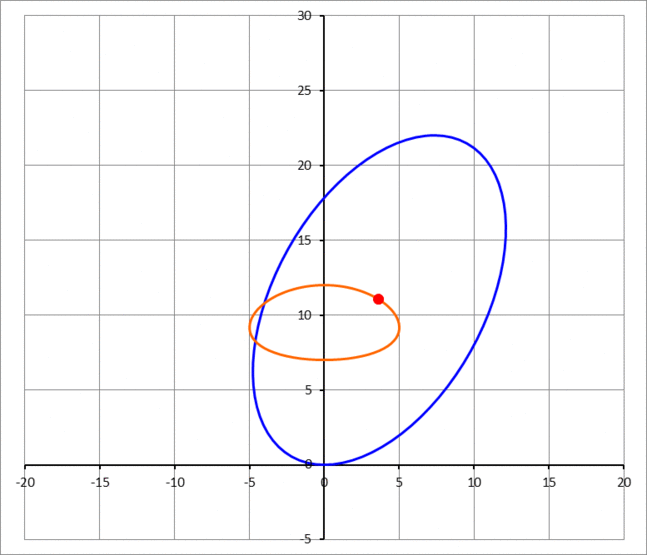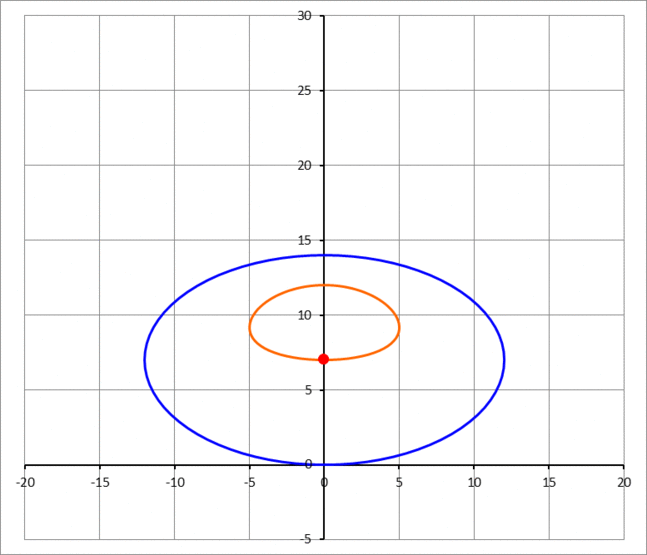
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Standard parametric equation of ellipse is ( a cos t , b sin t ) . Instead of letting center of ellipse move around, we will consider a scenario where center of ellipse is fixed at the origin of coordinate system S and where we set an origin of another coordinate system S' at some point on the ellipse such that its x'-axis coincide with tangent line to the ellipse at that point. So, radius vector of origin of S' with respect to S is ( a cos t , b sin t ) . Unit vector i ′ which corresponds to x'-axis is consequently: i ′ = t ^ = a 2 sin 2 t + b 2 cos 2 t 1 ( − a sin t , b cos t ) Unit vector j ′ which corresponds to y'-axis and is orthogonal to i ′ is then: j ′ = a 2 sin 2 t + b 2 cos 2 t 1 ( − b cos t , − a sin t ) Now, we can express origin of S with respect to S': O ′ O = − O O ′ = − a cos t ⋅ i − b sin t ⋅ j = a 2 sin 2 t + b 2 cos 2 t a cos t ( a sin t ⋅ i ′ + b cos t ⋅ j ′ ) − a 2 sin 2 t + b 2 cos 2 t b sin t ( b cos t ⋅ i ′ − a sin t ⋅ j ′ ) = a 2 sin 2 t + b 2 cos 2 t 1 ( ( a 2 − b 2 ) sin t cos t ⋅ i ′ + a b ⋅ j ′ ) Thus, curve which is traced by the center of ellipse is: ρ = a 2 sin 2 t + b 2 cos 2 t 1 ( 2 a 2 − b 2 sin 2 t , a b ) From here, it seemed to me a very tedious task to find a closed form expression for enclosed area, so I approximated the answer and matched it with the formula which is closest to it. However, I would like to know about a nice way to derive the formula, if it exists at all. @Hosam Hajjir ?