Area Of Cross - General Form
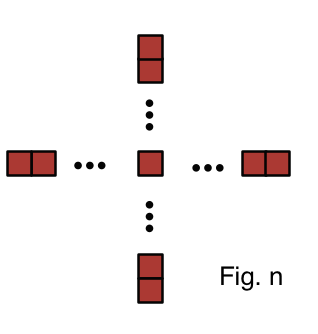 In figure number
n
, which of the following represents the number of squares that are present?
In figure number
n
, which of the following represents the number of squares that are present?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I did not get the answer ..Please explain it to me....
Log in to reply
use the formula a+(n-1)d. where a--- first term of the sequence, and d---- the common difference between the terms (succeeding number minus proceeding number).
It is a little hard to explain it without drawing... But the figure is like a star with 4 hands (this is where the 4n comes from), every time you count the number of squares on every hand you also count the square in the middle (the square that unites all the hands), so you have in fact counted it 3 times in addition, thus you need to subtract 3. And so the answer is 4n-3.
OK....you will need to have a basic knowledge of functions for this !!
We see that fig 1 has 1 square, fig 2 has 5 squares, fig 3 has 9 squares and so on. If you notice, you can see that in each successive figure, there is an increment of 4 squares (1 on each end of previous figure).
Let the figure no. be n . Then, if you set up a function f to find the area, the function f is defined like this ---->
f ( n ) = 4 ( n − 1 ) + 1
⟹ f ( n ) = 4 n − 4 + 1
⟹ f ( n ) = 4 n − 3 where n = Figure no. and f ( n ) = Area of figure n
It would help if one were able to figure out that n is not the number of squares per arm, but actually one less than that. I was able to guess the answer from the available assortment, but not from the formulation of the problem.
S n = a ( n − 1 ) + 1
where:
n = 1 , 2 , 3 . . . . . , ∞
a = 4
S n = 4 ( n − 1 ) + 1 = 4 n − 3
for n = 3 , S n = 9
- Initiation
"Un=Ua+(n-1)d"
- Unknown
a. Ua = 1 ... (i);
b. d = 4 ... (ii);
- Asked
Un=?
- Process
Un=Ua+(n-1)d <- (i) & (ii);
Un=1+(n-1)4;
Un=4n-3
here the pattern is 1,5,9,13.... so equation is 4n-3
4n-3, because it has 4 hands, but every time you count the 'hands' that means 4n you count the middle square in addition, so you need to subtract 3