Area Of Cross - Reversing It All

Algebra Level 1

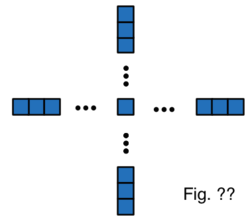If a figure in the pattern we've seen has 393 squares, what figure number will it have?


The answer is 99.

View wiki
Arron Kau by Arron Kau

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

13 solutions

Rituja Dikshit
Apr 17, 2014

4n-3=393 and 4n=396,n=99

8 Helpful 0 Interesting 0 Brilliant 0 Confused

Ok..!

Heder Oliveira Dias - 7 years, 1 month ago

Good one

TIRTHANKAR GHOSH - 7 years, 1 month ago

Tn=393

a=1

d=4

Tn=a+(n-1)*d

393=1+(n-1)*4

393=1+4n-4

396/4=n

99=n

n=99

1 Helpful 0 Interesting 0 Brilliant 0 Confused

well done !!! u made it luk like a A.P.

Shuvam Nayak - 7 years, 1 month ago

amazing man

Saaduddin Saad - 7 years, 1 month ago

💥 If a=1 💥 But it doesn't really say a=1 There isn't a clear explanation if the figure shown is the first in the set. Omit for ambiguity.

Lincoln Penaloza III - 5 years, 11 months ago
Somesh Singh
Apr 20, 2014

the figure number= no. of squares on each arm+1

given, total number of squares=393; removing central square=393-1=392 number of squares on each arm=392/4=98 therefore figure number=98+1=99

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Perihan Mohamed
Apr 17, 2014

4x - 3 = 393 4x = 393 +3 4x = 396 divide both sides by 4 x = 99

1 Helpful 0 Interesting 0 Brilliant 0 Confused

YEH

RAHUL PARMAR - 7 years, 1 month ago
Sahba Hasan
Jul 9, 2014

4n - 3 = 393

4n = 393 + 3

4n = 396

n = 396/4

n = 99

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Abhishek Rawat
May 23, 2014

tn=393,a=1,d=4 we know that, tn=a+(n-1)d by putting the above values we get, n=99

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Bro Jayanto
May 10, 2014

- Initiation

"Un=Ua+(n-1)d"

- Unknown

a. Ua=1...(i);

b. d=4...(ii);

c. Un=393...(iii);

- Asked

n=?

- Process

Un=Ua+(n-1)d <-(i),(ii),&(iii);

393=1+(n-1)4;

393=1+4n-4;

4n=396;

n= 396 4 \frac{396}{4} =99

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Carmen Labarta
Apr 23, 2014

x= 4n-3

393= 4n-3

393+3= 4n

396 = 4n

396/4 = n

n= 99

Therefore, the position is 99th

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Azurich Buscano
Apr 23, 2014

393=4n-3 (+3)+393 = 4n 396/4 = 4n/4 (to eliminate multiple n) 99=n (so, answer is 99)

0 Helpful 0 Interesting 0 Brilliant 0 Confused

4(n)-3=393, 4(n)=393+3, n=396/4= 99

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Isabella Amabel
Apr 20, 2014

a=1 ; d=4 ; a {n} = 393. Thus, n= (a {n}-a)/d +1 implies, (393-1)/4 +1 = 98+1 =99

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Yousuf Kamal
Apr 17, 2014

4n-3= 393. and 4n=393+3=396, Therefore n=396/4=99

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Sparsh Dutta
Apr 17, 2014

The solution can be acquired by the formula 4n-3=393 where n is the required answer

0 Helpful 0 Interesting 0 Brilliant 0 Confused

4n-3=393 so n=99

Khalid Choudhry - 7 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...