Area Of Cross - Starting Out

Algebra Level 1

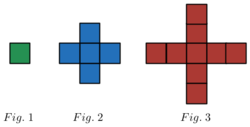We can easily count that figure 1 has 1 unit square and figure 2 has 5 unit squares. How many unit squares are present in figure 3?

This problem is part of Arron's set The Cross Investigations - Area .

9 5 8 11

View wiki
Arron Kau by Arron Kau

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

23 solutions

4x+1 (i)4(0)+1=1unit, (ii)4(1)+1=5units, (iii)4(2)+1=9

27 Helpful 0 Interesting 0 Brilliant 0 Confused

I just count it

Nguyễn Thị Hồng Miên - 7 years, 1 month ago

Log in to reply

FOR every increement 4 units are added on four sides .......thats it

Vamshi Kumar - 7 years, 1 month ago

any other idea on this?

maheswari mahalingam - 7 years, 1 month ago

1+4=5; 5+4=9

Gunasekaran Subbiah - 7 years, 1 month ago

Log in to reply

hello

muhammad azeem - 7 years, 1 month ago

one square = 1 cm square so we can sum the areas of the squares

hashem Shabbara - 7 years, 1 month ago

(x^2)/x

Tushar Chowdhury - 7 years, 1 month ago

Log in to reply

x

Maths Hunter - 7 years, 1 month ago

what's the rule man!!!!!!!!!!

Probal Raihan - 7 years, 1 month ago

every time if one unit is added to each direction, the number increases to 4, as it did in this case, or if we come to know how many are there in just one direction then multiply it by 4 and add 1= 4n + 1, so easy.

Dipen Katekhaye - 7 years, 1 month ago

just count it ...

Haris Sheikh - 7 years, 1 month ago

4x+1 (i)4(0)+1=1unit, (ii)4(1)+1=5units, (iii)4(2)+1=9

Dipak Bhosale - 7 years, 1 month ago

ans is 9

Kush Gupta - 7 years, 1 month ago

U1 = 1, U2 = 5, U3 = ?

Un = a + (n-1)b

a = 1, b = 5-1 = 4

U3 = 1 + (3-1)4 U3 = 1 + 2.4 U3 = 1 + 8 U3 = 9

Sa'adah Ca'em Lotus - 7 years, 1 month ago

ans is 9

Nisha Garg - 7 years, 1 month ago

9

Alauddin AL Azad Shipon - 7 years, 1 month ago

9

Ravindra Kumar Sonkar - 7 years, 1 month ago

9

Hasan Ahamed - 7 years, 1 month ago

9

Millat Afghan - 7 years, 1 month ago

9 without thinking . . .

Omar Khayyam - 7 years, 1 month ago

4n+1

Shailesh Patel - 7 years, 1 month ago

9

Venkatta Kumaran B - 7 years, 1 month ago

simply 9

Mukish Rahi - 7 years, 1 month ago

simple count..9

Mukish Rahi - 7 years, 1 month ago

9.. no more answers....

Honey Mae Cambarijan - 7 years, 1 month ago

9

Shahid Majeed - 7 years, 1 month ago

by counting

Foysal Hossain - 7 years, 1 month ago

9

Rizwan Ahmed - 7 years, 1 month ago

9

Ahmad Cheema - 7 years, 1 month ago

just count it

Idrees Ramzan - 7 years, 1 month ago

Simple 9

Muhammad Atif - 7 years, 1 month ago

9

Dhanireddy Amarnath - 7 years, 1 month ago

in figure third i am account there is 9 box

Iftikhar Shah - 7 years, 1 month ago

4=5=9

Helal Uddin - 7 years, 1 month ago

just count nd nothing

Harmain Rana - 7 years, 1 month ago

just 9

Neethu Thomas - 7 years, 1 month ago

jst count it is 9

Neethu Thomas - 7 years, 1 month ago

9

Elle manzey - 7 years, 1 month ago

9

Sruthi Gpillai - 7 years, 1 month ago

wat a simple question????.

Abhijit Kollathodiyil - 7 years, 1 month ago

so, how it's gonna be the 3rd square?

James Sinambela - 7 years, 1 month ago

simply count it

Rabia Qayyum - 7 years, 1 month ago

5+4=9

Rizky Ramadhani - 7 years, 1 month ago

49-49=49

syed abdul manan zafar - 7 years, 1 month ago

i just counted the box ..

Abid Ali - 7 years, 1 month ago

11 is a corret answer

Pankaj Kumar Mishra - 7 years, 1 month ago

9

Manav Bhalla - 7 years, 1 month ago

9 unit sq.

Lubna Shahid - 7 years, 1 month ago

i know the formula :)

Christopher Canlas - 7 years, 1 month ago

it has 4 side square box which contain 2 small box and it also have one centre box soo 4*2=8 , +1

Shahroz Ahmed - 7 years, 1 month ago

Just counted it

Pilol Kumang - 7 years, 1 month ago

This was the dumbest question for the level we are rated for - my answer was correct yet directed to the solution...

Phani SV - 7 years, 1 month ago
Thankaraj P
Apr 17, 2014

1,5,9,......
Difference(d) is 4 First term(a) is 1 3rd term = ? a+(n-1)d= 1+(3-1)4 = 1+8 = 9

2 Helpful 0 Interesting 0 Brilliant 0 Confused

same solution,i was thought

RITUJA DIKSHIT - 7 years, 1 month ago
Omar Nader
Jul 26, 2014

count the unit

1 Helpful 0 Interesting 0 Brilliant 0 Confused

We can find here an arithmetic progression: the initial term is 1 and the common difference is 4. So, a 3 = a 1 + 2d = 1 + 2\times 4 = 1 + 8 = 9

1 Helpful 0 Interesting 0 Brilliant 0 Confused
M Shariq Sohail
Apr 17, 2014

5+4=9

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Paul Tan
Jun 11, 2014

X= no. Of squares.

Figure 1. X=1

Figure 2. X= 1+4

Figure 3. X= 1+4(2)

Figure 4. X= 1+4(3)

So on and on.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Sabbir Hossain
May 16, 2014

Suppose, X=figure no(0 to 2) & Law is 4x+1. 

  So (i) (4*0) +1=1 Squire, (ii) (4*1)+1=5 Squire, (iii) (4*2)+1= 9 Squire.
0 Helpful 0 Interesting 0 Brilliant 0 Confused
Siddharth Singh
May 13, 2014

Just count the unit squares and DON'T count that squares which you have counted earlier....ENJOY.......!!!

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Saleem Usman
Apr 29, 2014

4x+1 (1),4(0)=1 (2),4(1)+1=5 (3),4(2)=9

)

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Anjali P
Apr 28, 2014

very simple.i am expecting some more difficult

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Dladla Arthur
Apr 28, 2014

arithmetic sequence of difference =4

add 4 unit squares to previous figure

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Arwinth Gabriel
Apr 28, 2014

1+4=5 ; 5+4=9

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Mona Mazen
Apr 27, 2014

9 number of squares + number of squares-1 =5+4

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Milena Lee
Apr 27, 2014

4n-3

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Subramaniam Gsm
Apr 26, 2014

i just counted it manually :)

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Bushra Khurshid
Apr 26, 2014

1+4=5+4=9

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Foysal Hossain
Apr 24, 2014

by counting

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Azurich Buscano
Apr 23, 2014

start as 1, then add all corners (equivalent of 4). So, the first answer is 5. then add corners again (it means add 4 again) the final answer is 9.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Hien Nguyen
Apr 18, 2014

I think :1+4+4= 9

0 Helpful 0 Interesting 0 Brilliant 0 Confused
HRitesh Dubey
Apr 17, 2014

1 box= 1unit....... then 9 boxes=9unitsqr.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

In this series 1,5,.......

First term (a) is 1. First term and Secind term differnse is 4. Differense (d) = 4.

Tn=a+(n-1)*d

T1=1+(1-1)*4

T1=1

T2=1+(2-1)*4

T2=5

T3=1+(3-1)*4

T3=9

In 3 squire total 9 units are present

0 Helpful 0 Interesting 0 Brilliant 0 Confused

that is stupid just count the squares

shalin hannens - 7 years, 1 month ago

9 units

Khairil Safli Pohan - 7 years, 1 month ago
Shafit Vohra
Apr 17, 2014

Its so simple..... no of squares is equal to {4(n-1) + 1} where n will be number of squares in any one of the four arms of figure (including center square too)

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Mukhtar Ahmad
Apr 17, 2014

if Nx = # of rows and Ny-=No columns then Nx X Ny-(Nx-1)X(Ny-1)

0 Helpful 0 Interesting 0 Brilliant 0 Confused

nine unit square contains in figure 3...

NITISH KUMAR - 7 years, 1 month ago

As easy as drinking wine simply answer is 9 bcs. this figure include 9 blocks

Gyan Pratap - 7 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...