Area Of Cross - Way Out There
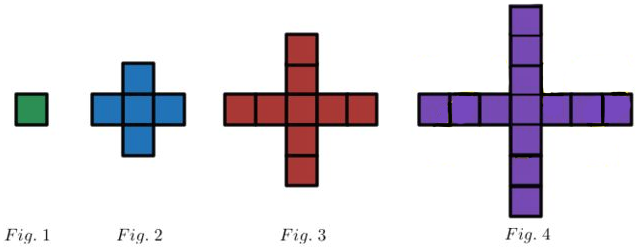 How many squares are present in figure number 20?
How many squares are present in figure number 20?
The answer is 77.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
52 solutions
In the first diagram there are no legs on the center block. In the second diagram there is one block on each of four legs. Third diagram three blocks on each leg. Fourth leg to have 4 blocks?linear progression total of 13.
Awesome solution.
Each arm of the cross has n-1 squares; add the 1 in the middle and the number of squares N = 4(n-1) +1
Excellent and concise solution.
f(n)=1+4(n-1). The original square(1) has four sides(4) f(1)=1, f(2)=5, etc.
Easily understandable.
If we observe the pattern of the number of squares, it forms an arithmetic progression given by 1,5,9,13,17, and so on whose n th term is given by a n = a + d ( n − 1 ) .
Here, n = 2 0 , a = 1 , and d = 4 , so a 2 0 = 1 + 4 ( 1 9 ) = 7 7 .
Imagine a "figure 0". This figure would have a value of -3 squares because "figure 2" has 5; 4 more than "figure 1". "Figure 0" therefore has the value of squares in "figure 1" minus 4, which is -3.
Now we know that "figure 0" has a value of -3 squares which also is the value of "m" in the function: f ( x ) = k x + m By looking at "figure 1" for example, we can now see that k = 4. To explain:
f ( x ) = k x − 3 f ( 1 ) = k ∗ 1 − 3 k − 3 = 1 k = 4
Everything that's needed to calculate the answer of f(20) is now available!
f ( x ) = 4 x − 3 f ( 2 0 ) = 4 ∗ 2 0 − 3 = 8 0 − 3 = 7 7
Answer: 77
1 is constant throughout. The outer series is 0,4,8,12,.. and so on. which can be written as (n-1) 4.... so no of squares in Fig.n - 1+ (n-1) 4
follow the sequence:1, 5, 9, 13,.............(4n-3)
so, the 20th term will be =(4 x 20 -3)=77
there is 1 square in the centre. 1st pattern = 1 in the centre 2nd pattern = 1 in the centre, 1 square each side (there are 4 sides) 3rd pattern = 1 in the centre, 2 squares each side (there are 4 sides) . . , so, side = n => 4(n-1) + 1 => U20 = 4(20-1) + 1 = 4(19) + 1 = 76 + 1 = 77
The number of squares are in AP. So Tn= a+(n-1)d Tn=1+(19*4) Tn=77
Each step adds 4 to the initial 1 block. Therefore the 20th step will add 1 + (19 x 4) = 77.
4 is the difference and then 1 4-1=3 so 4 20=80-3=77
In Fig. n, each "arm" has n-1 blocks. There is one square in the centre. So the number of squares in the figure is 4(n-1)+1
So in fig 20, there are 4(20-1)+1 squares = 4x19 +1=77
1+4(n-1) IS THE nTH TERM OF THE SEQUENCE. This = 4N-3 (4(20)-3=77.)
1: 1 , 2: 1 + 4 = 1+(2-1)x4, 3: 1 + (2-1)x4 + 4= 1+(3-1)x4, ..., 20: 1 + (19-1)x4 + 4 = (20-1)x4 => 77
I used (N-1)*4+1. 4 sides of n-1 plus the center square. which also reduces fo 4n-3
Think of figure 1 as figure 0, figure 2 as figure 1, figure 3 as figure 2, figure 19 as figure 20, figure n as figure n − 1 and so on. (Basically, number the set like a programmer and not like a mathematician.)
Once you do this a formula falls out:
n s q u a r e s ( 0 ) = 1 + ( 4 × 0 ) = 1 + 0 = 1
n s q u a r e s ( 1 ) = 1 + ( 4 × 1 ) = 1 + 4 = 5
n s q u a r e s ( 2 ) = 1 + ( 4 × 2 ) = 1 + 8 = 9
n s q u a r e s ( 3 ) = 1 + ( 4 × 3 ) = 1 + 1 2 = 1 3
∴
n s q u a r e s = 1 + ( 4 n f i g u r e )
∴
n s q u a r e s ( 1 9 ) = 1 + ( 4 × 1 9 ) = 1 + 7 6 = 7 7
the first figure has 0 square under itself, the second has 1, third has 2,... 20th has 19. Then 19x4+1 = 77.
All I did was just the formula of arithmetic progression. Just examine the sequence then derive it to a=1, n=20, and d=4. So (20th term)=(1st term)+(n-1)(d)=1+19*4= 77 .
Fig (1): 1, Fig (2): 5, Fig (3): 9, Fig (4): 13, : : We see the recurrence sequence: Fig (1)=1, Fig (N+1)=Fig (N)+4.
From this we get: Fig (N+K)=Fig (N)+Kx4.
Taking N=1 and K=19, we get Fig (20)=Fig (1)+19x4=1+19x4=77.
well each new figure the blocks on the outside from the center point extend by 1... so 19 times 4 plus 1
new fig number = fig number-1 new fig number×4 +1 20-1=19 19×4+1=76+1=77
Its just an A.P with first term =1 and common difference =4. So 20th term implies 1 + (20-1)4 = 77.
S n = a ( n − 1 ) + 1
where:
n = 1 , 2 , 3 . . . . . , ∞
a = 4
for n = 2 0 , S n = 7 7
Call fig (n). Fig 1. Squares = 1 + 4 x (n - 1) = 1 + 4 x 0 = 1 Fig 2. Squares = 1 + 4 x (2 - 1) = 1 +4 = 5 .... Fig 20. Squares = 1 + 4 x (20 - 1) = 1 + 4 x 19 = 1 + 76 = 77
I kind of went about it in a more convoluted way, but whatever. I will let f be the figure number, and n be the amount of squares. Then f is one, there is one square, and every one after that adds four squares. Logically, we can deduce that n can be determined by n=4(f-1)+1 which can be simplified to n=4f-3 with this, it's simple substitution. n=4(20)-3 n=80-3 n=77
Figure 1 is one square. The # squares for each figure follows an arithmetic progression, with a_1 =1, d=4, and the problem asks for the # squares in figure 20 (n=20).
The recursive formula for the # of squares in figure n = a (n+1) = a n + 4 The explicit formula for the # of squares in figure n = 4n-3 = 1+4(n-1)
An interesting problem someone could make out of this would be
What is the sum of all the squares from figures 1 through 20, inclusive?
By symmetry, 1+5+9+13+17+21+...77 = (77+1)*(20/2) = 780
Sum from n=1 to n= 20 of (4n-3) = 4*sum from n=1 to n=20 of n - sum from n=1 to n=20 of 3 = 4 * (20(20+1))/2 - 3(20) = 840 -60 = 780
It is readily observed that each cross after the first has four more units of area than its predecessor. Hence, the sequence of areas form an arithmetic progession with initial term a = 1 and common difference d = 4. A formula for the area of the nth such cross is then 1 + 4(n - 1). In our case n = 19 (as the sequence is indexed from zero) and we obtain 1 + 4(19 - 1) = `1 + 76 = 77.
Moderator note:
Simple standard approach.
a=1, d=4, n=20 a+(n-1)d =1+(20-1)4=1+19x4=1+76=77
a+(n-1)*d a=first element. d=distance between two consecutive element. n=Number of position of square,
simple
1+[4*(n-1)],
n=fig no.
I just thought (0x4)+1 is first one, so (1x4)+1, and so on. For 20 its (19x4)+1. Bingo.
Each arm of the cross contains (fig minus 1) squares. Added to the centre square gives the formula T=4(fig-1)+1. So if fig=20, T= (4x19)+1 = 77.
4 x (figure number - 1) + 1
or
Arithmetic Progression
a + (n - 1) d
whereas,
a = first term
n = nth term
d = difference among the numbers in the sequence
or
you can just simply study this:
Figure 1 = 1
Figure 2 = 5
Figure 3 = 9
....
....
....
Figure 18 = 69
Figure 19 = 73
Figure 20 = 77
3(n-1)+n ,where n=figure number. 3(20-1)+20=3x19+20 => 57+20=77 P.S formula made just for this question. xD😁😁
Number of Sqr in nth figure= (n-1)*4+1
Arithmetic sequence with a common difference of 4. Formula: a + (n-1)d.
20 is the number of squares of the cross, right upto the centre. subtracting 1 square from 20, we get the number of squares in each of the remaining arms of the cross, not including the centre, of course. thats 20 + 19 +19 +19 = 77 this is probably the simplest approach.no formulae.
pattern is 1,5,9,13----- so (4n-1) when n=20 we get 77.
I analyzed it and the box increases by 4 in every cross so my solution is
1+[19(4)] = 77 :D
20 - 1= 19 19 * 4 = 76 76 + 1 = Answer . Ok and Easy.
If we observe the pattern of the number of squares, it forms an arithemetic progression given by 1,5,9,13,17......and so on whose nth term is given as: N= a+(n-1)d where n is the number of term (i.e no of fig), a is the first term (=1) and d is the common difference(=4) and the result N will give the number of squares in the fig corresponding to number n. here, n=20, a=1,d=4 hence, N=1+(20-1)4=77
looking to figures we finf that each figure ha one lower no of square on each side plus one centre square. thus 20 th figure will have 19 x4 plus 1 that is 77 Ans
K.K.GARG,India
a=1; n=20; d=4. Thus, a_{n} = a+(n-1)d = 1+ 19*4 =77
The number of boxes in each figure is in AP. Thus we can find the t20, which is to say the number of boxes in fig. 20 by using the formula : tn= a + (n-1) d. taking 'a' as the first term of the A.P, a=1, d= the difference between consecutive terms = 4 tn= a+(20-1) 4 tn= 1+ 76 tn=77
the equation will be ( 4x - 3 ) and x is the number of the figure .. so x = 20 ,, therefore 4(20)-3 = 77
(4(figure number -1) +1) SO (4(20-1)+1)= 77
Number of Squares = 1+ ( (n-1) * 4 ) where n= figure number; For figure 20, 1+ ( 19 * 4 ) = 77
4n-3=4x20-3=77
congratulation
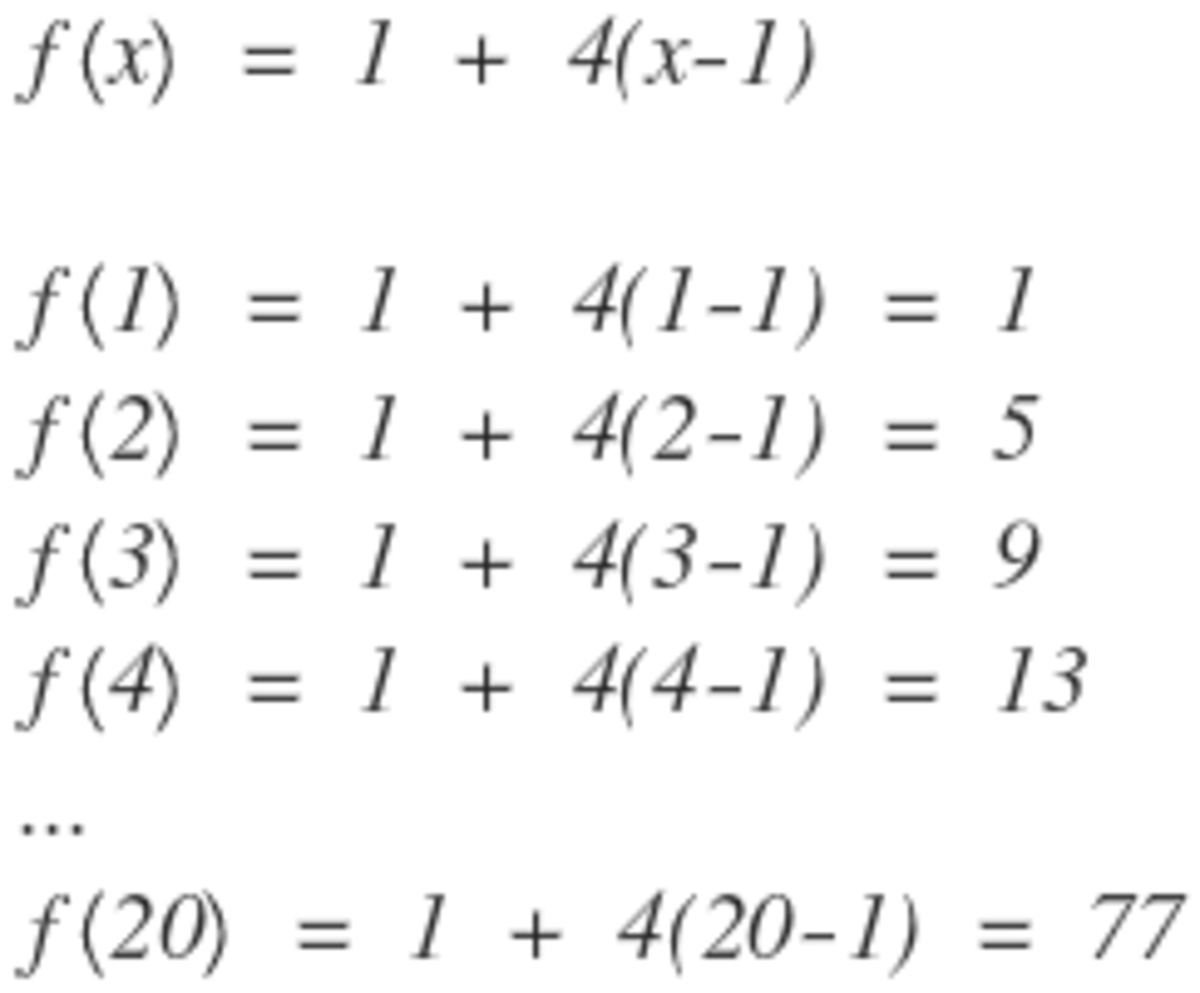
Examine the initial terms in the sequence: 1, 5, 9, 13, ...
We can deduce that the n th term in the sequence is given by 4 n − 3 . Therefore, the 20th term is 4 ( 2 0 ) − 3 = 7 7 .