Area of Figure with Three Circles
A figure consists of three circles each with a radius of 5 drawn such that each circle has a tangent with another circle(s) center. What is the area of the figure? Give your answer correct to the nearest whole number.
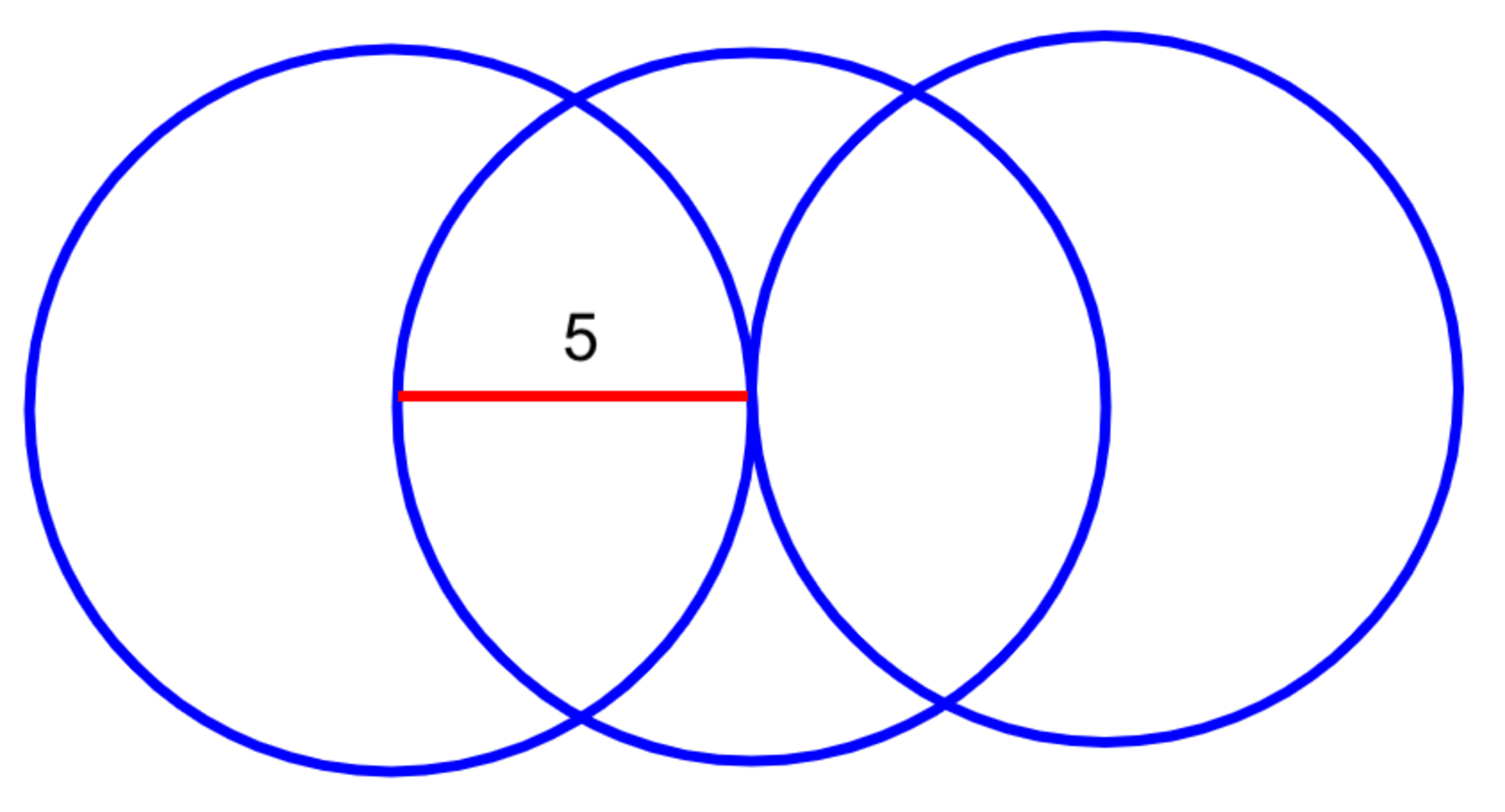 Figure
Figure
The answer is 174.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The area of one overlapping section is comprised of one 60º circle sector (A + B) and another smaller section (B). Since 6 0 º is one-sixth of the circle, the area of (A + B) is 6 1 ⋅ π ( 5 ) 2 = 6 2 5 π .
Now area B is equal to the 60º circle sector (A + B) minus the equilateral triangle (A). We have just found area (A + B), but we don't know the area of the equilateral triangle. One way to do this is to first find its height. This is just 5 2 − ( 5 / 2 ) 2 = 2 5 3 by Pythagoras, so the area is 2 1 ⋅ 5 ⋅ 2 5 3 = 4 2 5 3 . So area B is (A + B) - A, or just 6 2 5 π − 4 2 5 3 . Other methods such as using the formula Area = 2 1 a b sin C , or using trigonometry to find the height of the triangle give the same answer.
The area of one overlapping section is now (A + B) + B, which equals 6 2 5 π + 6 2 5 π − 4 2 5 3 = 2 ⋅ 6 2 5 π − 4 2 5 3 . Now back to the original problem. If we add the areas of the three circles together, then we will have double-counted four of the overlapping sections. Consequently, we need to subtract the area of the four overlapping sections from the 3 circles to get the area of the entire figure. This is just 3 ⋅ π ( 5 ) 2 − 4 ( 2 ⋅ 6 2 5 π − 4 2 5 3 ) = 1 7 4 . 2 0 ⋯ , which when rounded to the nearest integer gives 1 7 4 .