Area of intersection of four circles!
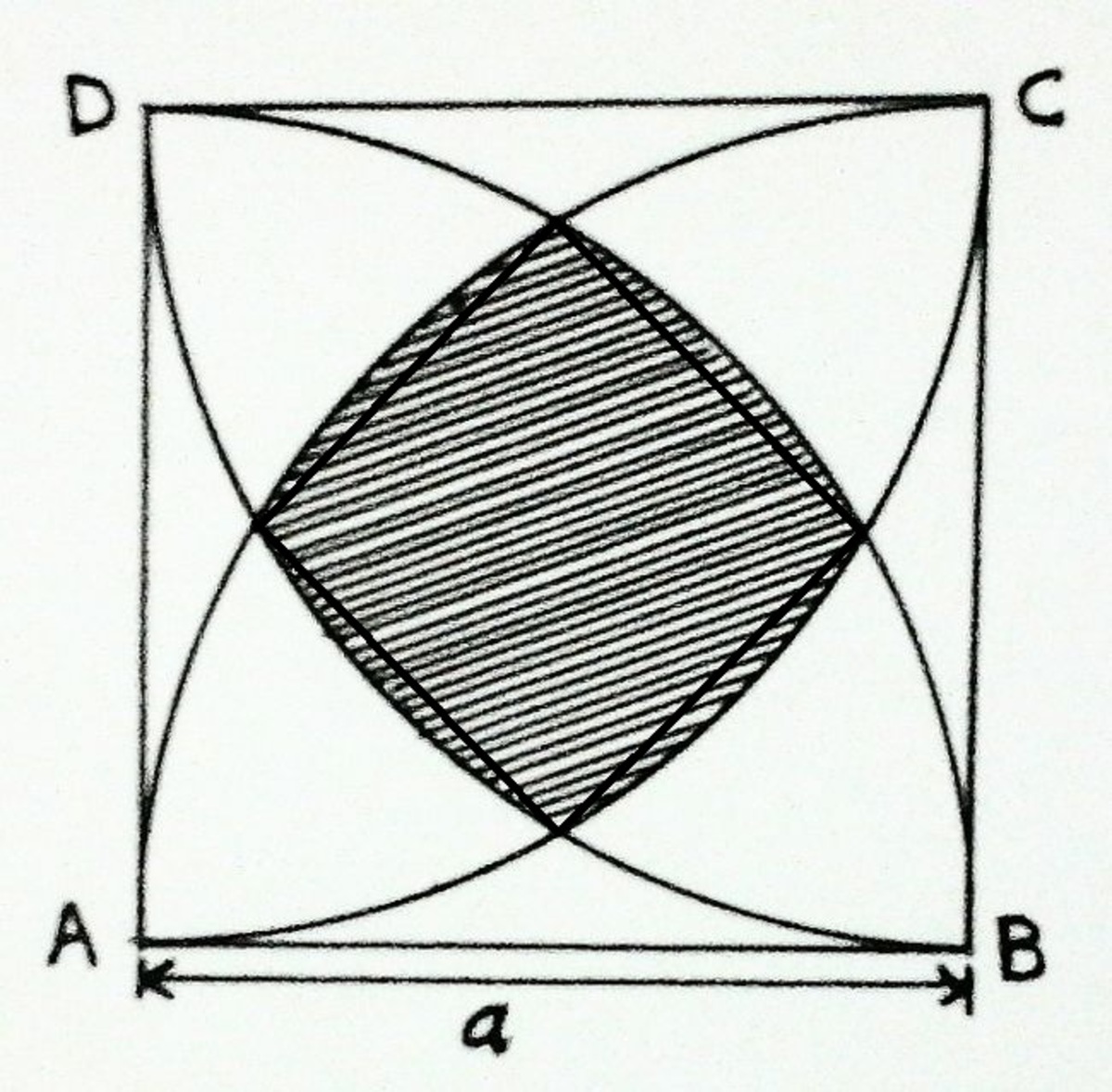
 The diagram above shows a square
with each side a. Four circles, each with radius a are centered at the vertices
of the square. If
then find out the shaded area (in
) of intersection of these circles. Give your answer to 3 decimal places.
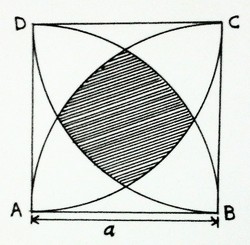
The diagram above shows a square
with each side a. Four circles, each with radius a are centered at the vertices
of the square. If
then find out the shaded area (in
) of intersection of these circles. Give your answer to 3 decimal places.
The answer is 45.38113108.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
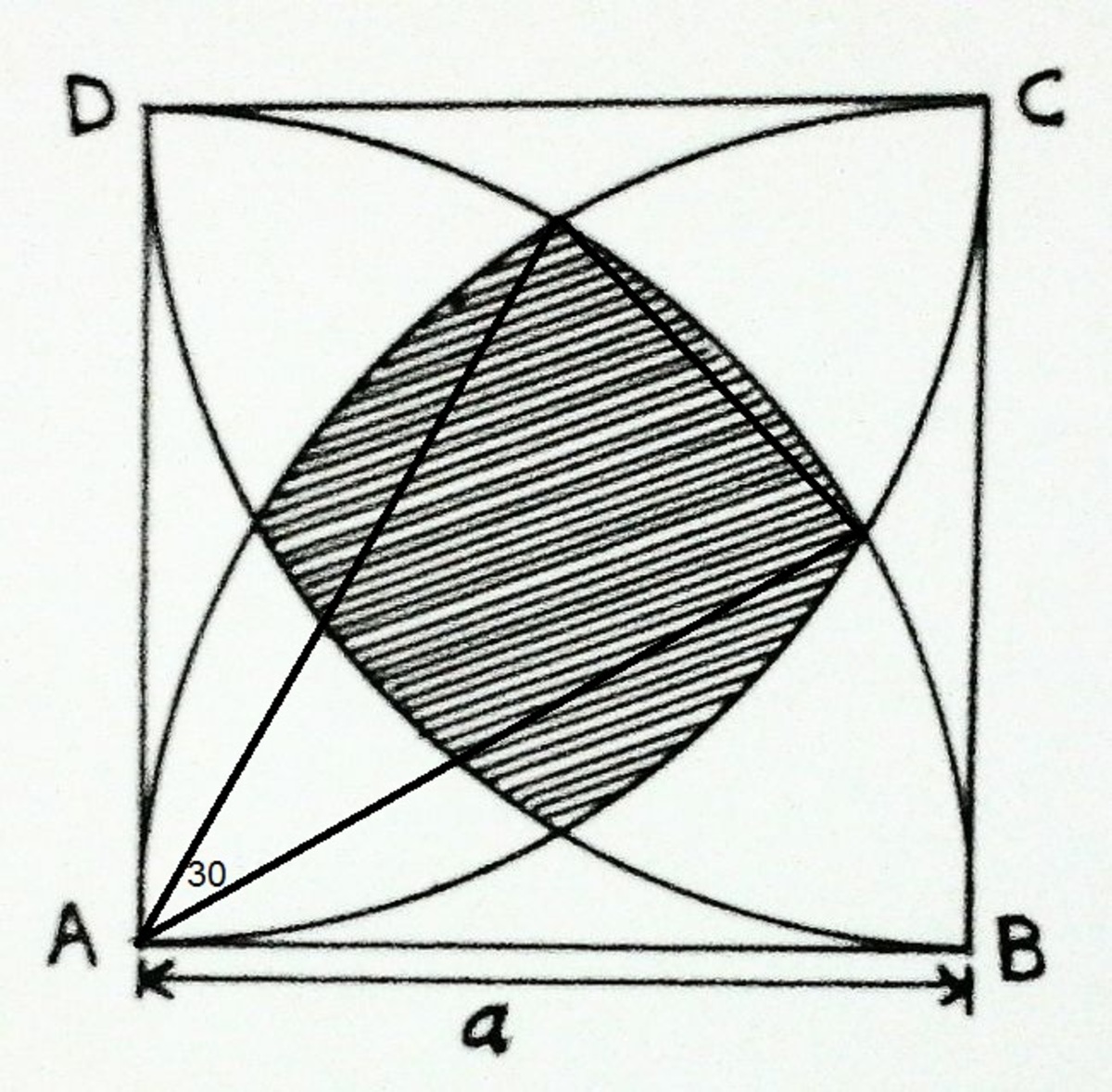 you can do that to get the four parts.. then add the square
you can do that to get the four parts.. then add the square