Area of intersection of two ellipses
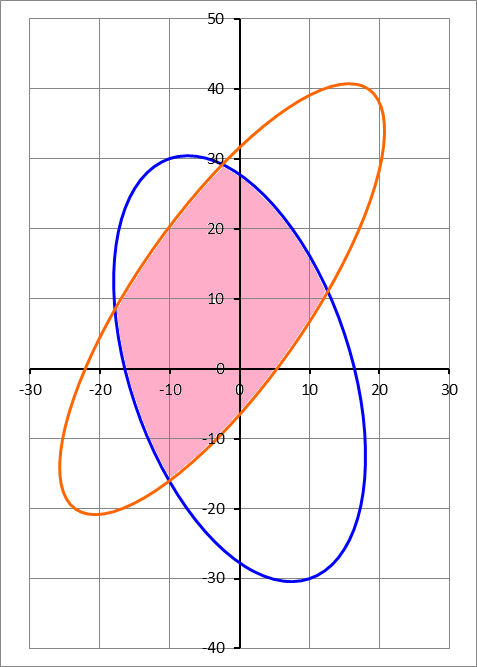
Two ellipses are drawn on the Cartesian plane, the first (blue) is centered at , and has a semi-major axis congruent with the vector , and a major to minor axis length ratio of 2 (i.e. the minor axis is one half the major axis). The second ellipse (orange) is centered at and has its semi-major axis congruent with the vector , and a major to minor axis length ratio of 3. Find the area of intersection (shaded in pink) between the two ellipses.
The answer is 787.36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here's a messy, brute-force solution. The problem is flagged as geometry, but I definitely resorted to calculus, which makes me think there's a better way to do this!
The general equation for a conic section in Cartesian coordinates is A x 2 + B x y + C y 2 + D x + E y + F = 0 . For an ellipse with semi-major axis a , semi-minor axis b , centre ( x c , y c ) and with its major axis an angle θ from the positive x -axis, these coefficients are
A B C D E F = a 2 sin 2 θ + b 2 cos 2 θ = 2 ( b 2 − a 2 ) sin θ cos θ = a 2 cos 2 θ + b 2 sin 2 θ = − 2 A x c − B y c = − B x c − 2 C y c = A x c 2 + B x c y c + C y c 2 − a 2 b 2
(these can be derived by applying coordinate transforms to an ellipse centred at O with its axes on the coordinate axes, or found here )
Using the given information, for the blue ellipse, we have
x c a 2 b 2 cos θ sin θ = y c = 0 = 1 0 2 + ( − 3 0 ) 2 = 1 0 0 0 = ( a / 2 ) 2 = 2 5 0 = 1 0 2 + ( − 3 0 ) 2 − 1 0 = 1 0 − 1 = 1 0 2 + ( − 3 0 ) 2 3 0 = 1 0 3
Substituting in and cancelling common factors, we get the equation 3 7 x 2 + 1 8 x y + 1 3 y 2 − 1 0 0 0 0 = 0 for the blue ellipse.
In the same way, we find 3 7 9 6 x 2 − 4 4 8 0 x y + 2 1 6 4 y 2 + 6 3 7 8 0 x − 5 4 4 8 0 y − 4 4 7 1 1 1 = 0 for the orange ellipse.
These implicit equations can be thought of as quadratics in the variable y ; for example, the equation for the blue ellipse can be solved for y to give
y = 1 3 ± 2 0 3 2 5 − x 2 − 9 x
For simplicity, let's call these two solutions y = B + ( x ) and y = B − ( x ) and define y = O + ( x ) and y = O − ( x ) for the orange ellipse in the same way.
Here I started using numerical methods. The equations can be solved to find the four points where the ellipses intersect; these are ( − 1 7 . 8 6 , 8 . 5 4 ) , ( − 1 0 . 0 8 , − 1 6 . 0 2 ) , ( − 2 . 5 1 , 2 9 . 2 0 ) and ( 1 2 . 6 3 , 1 1 . 0 6 ) . Call these X i , Y i for i = 1 , 2 , 3 , 4 . Using these, the pink area can be divided into three distinct regions, as below:
The red region is bounded by y = O + above and y = B − below, so its area is
∫ X 1 X 2 ( O + − B − ) d x ≈ 1 6 7 . 2 2
Similarly, the green area is
∫ X 2 X 3 ( O + − O − ) d x ≈ 2 8 5 . 6 0
and the yellow area is
∫ X 3 X 4 ( B + − O − ) d x ≈ 3 3 4 . 5 4
These integrals can be computed analytically, but I went with numerical methods. Summing, we get the answer: 1 6 7 . 2 2 + 2 8 5 . 6 0 + 3 3 4 . 5 4 = 7 8 7 . 3 6