Area of Morley's Triangle
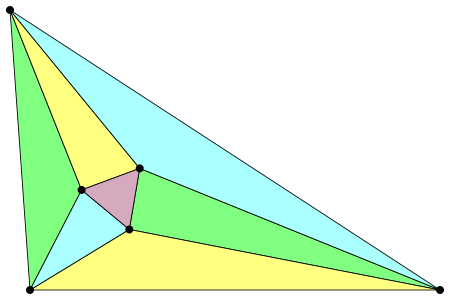The image above is an illustration of what is known as Morley's Theorem. It states that if the angles of any triangle are trisected and the lines extending from these trisections are connected as shown above, then the triangle made by those connections will be equilateral. Such equilateral triangles are known as
First Morley Triangles
. Observe the following image:
The triangle shown above is a 45-45-90 triangle with a hypotenuse of length 4. If the area of the First Morley Triangle depicted in this image can be written as a b − c , where a , b , and c are positive integers and b is square-free, what is a + b + c ?
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Did the same way. For isosceles right triangle, R=1/2 * Hypotenuse .
The side of the required equilateral triangle is given by :
8 R sin 3 A sin 3 B sin 3 C = 4 ( 4 ) sin 2 1 5 sin 3 0 = 8 sin 2 1 5 = 4 ( 1 − cos 3 0 ) = 4 ( 1 − 2 3 ) = 2 ( 2 − 3 )
Thus Area of the triangle:
A = 4 3 × 2 2 ( 2 − 3 ) 2 = 3 ( 4 − 4 3 + 3 ) = 4 3 − 1 2 + 3 3 = 7 3 − 1 2
So the answer must be 7 + 3 + 1 2 = 2 2
Can you say how you got the first line. Proof? I did it using sine rule and finally cosine rule.
Log in to reply
Look at Morley Triangle It gives the formula for the area. The Diameter of the circumscribed circle is the length of any side divided by the sin of the opposite angle : Circumscribed triangle
Let r be circumradius of △ A B C ,
α = ∠ A / 3 , β = ∠ B / 3 , γ = ∠ C / 3
Side of a Morley triangle is:
s = 8 r ∗ s i n ( α ) s i n ( β ) s i n ( γ ) = 8 ∗ 2 ∗ s i n ( 3 0 ) s i n ( 1 5 ) s i n ( 1 5 ) = 4 − 2 3 A r e a = 4 3 s 2 = 7 3 − 1 2 ⇒ a + b + c = 2 2