Area of My Valentine
Find the area of the heart-shaped region bounded by the equation x 2 + ( 4 5 y − ∣ x ∣ ) 2 = 1 to six decimal places.
The answer is 2.513274.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
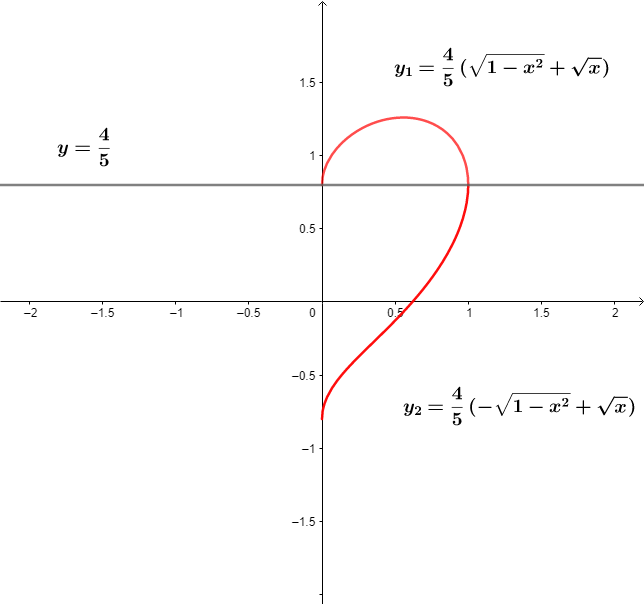
A 1 = 5 4 ∫ 0 1 ( 1 − x 2 + x − 1 ) d x = 5 4 ( ∫ 0 2 π cos 2 d θ + ∫ 0 1 x − 1 d x ) = 5 4 ( 2 1 ( θ + 2 1 sin ( 2 θ ) ) ∣ 0 2 π + ( 3 2 x 2 3 − x ) ∣ 0 1 ) = 5 4 ( 4 π − 3 1 )
Similarly, A 2 = 5 4 ∫ 0 1 ( 1 + 1 − x 2 − x ) d x = 5 4 ( ∫ 0 2 π cos 2 d θ + ∫ 0 1 1 − x d x ) = 5 4 ( 2 1 ( θ + 2 1 sin ( 2 θ ) ) ∣ 0 2 π + ( x − 3 2 x 2 3 ) ∣ 0 1 ) = 5 4 ( 4 π + 3 1 )
⟹ A 1 + A 2 = 5 2 π ⟹ the area of the heart A = 2 ( A 1 + A 2 ) = 5 4 π ≈ 2 . 5 1 3 2 7 4 .
Since you want the sum A 1 + A 2 , you can simply add the integrands 5 4 ( 1 − x 2 + x − 1 ) and 5 4 ( 1 − x 2 − x + 1 ) to get 5 8 1 − x 2 , and take it from there.
x 2 + ( 4 5 y − ∣ x ∣ ) 2 x 2 + ( 4 5 y − x ) 2 4 5 y − x y = 1 = 1 = ± 1 − x 2 = 5 4 ( x ± 1 − x 2 ) For x ≥ 0 ∣ x ∣ = x
We note that y has two parts y = 5 4 ( x + 1 − x 2 ) , the blue curve, and y = 5 4 ( x − 1 − x 2 ) , the red curve. The area of half the heart A = ∫ 0 1 y d x also has two parts A 1 = ∫ 0 1 5 4 ( x + 1 − x 2 ) d x , the blue + purple regions, and A 2 = ∫ 0 1 5 4 ( x − 1 − x 2 ) d x , the pink + purple regions. And that:
A = A 1 − A 2 = ∫ 0 1 5 4 ( x + 1 − x 2 ) d x − ∫ 0 1 5 4 ( x − 1 − x 2 ) d x = 5 8 ∫ 0 1 1 − x 2 d x = 5 8 ∫ 0 2 π cos 2 θ d θ = 5 8 ∫ 0 2 π 2 1 + cos 2 θ d θ = 5 4 [ θ + 2 sin 2 θ ] 0 2 π = 5 2 π Let x = sin θ ⟹ d x = cos θ d θ
Therefore, the area of the heart = 2 A = 5 4 π ≈ 2 . 5 1 3 2 7 4 .