Area of outside region
A line segment is 50 units long and intersects a circle tangentially at one of it's endpoints. The line is then revolved around the circle remaining tangent, and keeping it's endpoint on the circle as it is revolved, creating a loop that completely encloses the inner circle, as shown in the diagram below. Find the area of the outside region created by the revolution. Use 3.14 for pi if necessary.
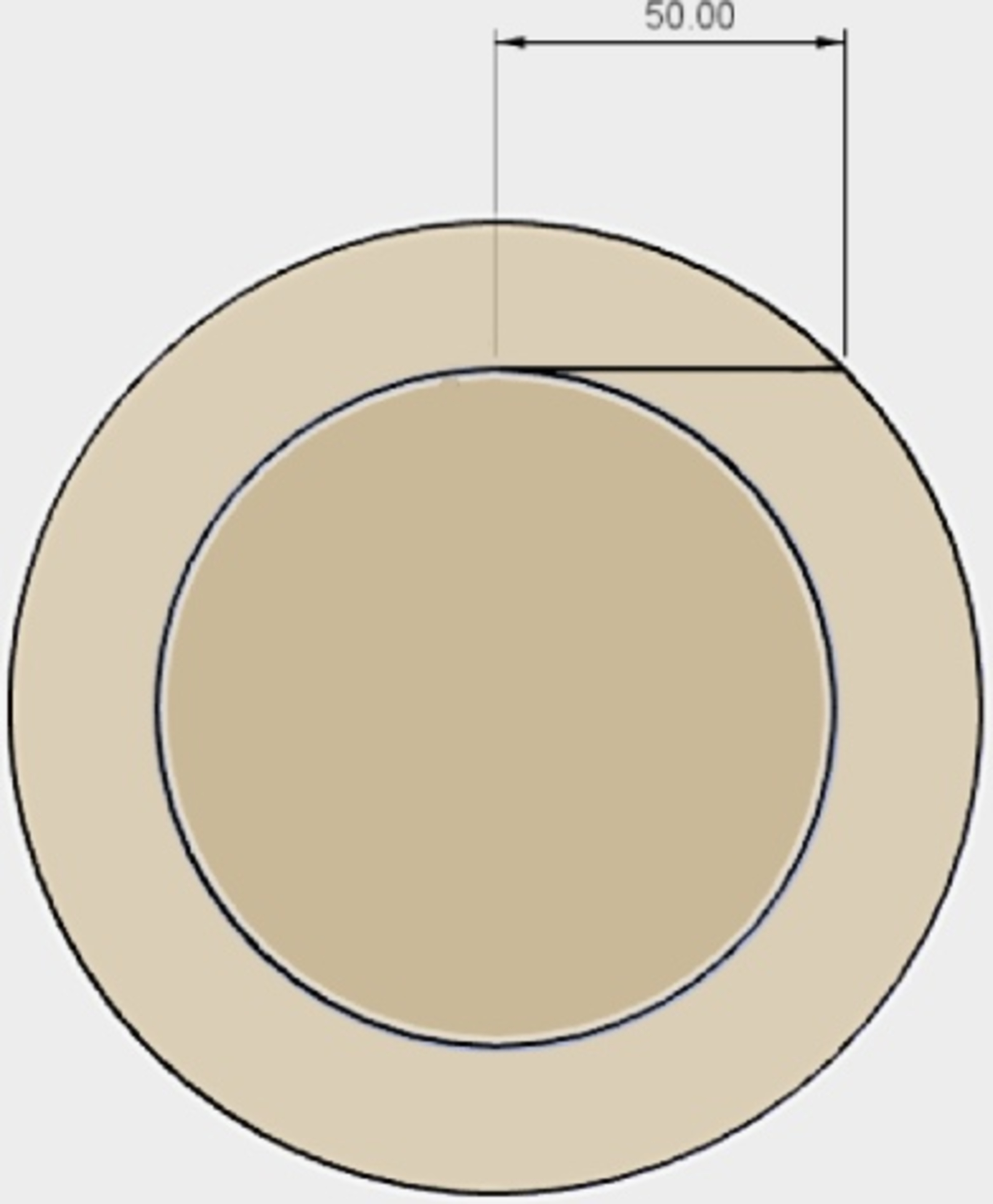
The answer is 7850.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To get the outside area you need to subtract the area of the inside circle from the area of the outside circle. Since you are not given a radius, consider the inside circle to have a radius denoted r, and the outside area to have radius R. Since the tangent line in perpendicular to the radius, you can solve for R in terms of r with the pythagorean theorem.
Outside radius (R)
= sqrt(r^2 + 50^2) pythagorean theorem
= sqrt(r^2 + 2500)
Area of the outside circle
= 3.14(R)^2
= 3.14(r^2 + 2500)
= 3.14(r^2) + 3.14(2500)
= 3.14(r^2) + 7850
Area of inside circle
= 3.14(r^2)
So, the area of the outside region
= Area of outside circle - Area of inside circle
= 3.14(r^2) + 7850 - 3.14(r^2)
= 7850
Generalizing this, the outside ring measured tangentially from the inside circle with a measure along the tangent of x is equal to pi(x)^2, the same as a circle, and does not depend on the inside radius. As the inside radius increases, it covers a larger circumference, but the inside circle will get closer and closer to the outside one, and so the outside ring will become thinner.