Area of parallelogram $ABCD$

It is not a rigorous proof, but rather interesting. Fold the figure, as shown. We will see the area of the parallelogram is twice of the rectangle's, or equivalently, 4 times of the square's. Hence the area of parallelogram is $4\times 144 = 576$ .

Of course, to make it rigorous, we have to make sure that (i) edges are not overlapping (ii) no any uncovered area, after folding. (Will continue it tonight or tomorrow...)

Using analytic geometry: Let (0,0) be the center of the figure. Then the four corners of the blue rectangle are (-12,6), (12,6), (12,-6) and (-12,-6).

Using the green squares, we can see the slope of line AD (and also line BC) is 1/2.
Using the red squares, we can see the slope of line AB (and also line CD) is -1/3.

Use algebra to find the four vertices of the larger parallelogram A: (-2.4,10.8), B (26.4,1.2), C (2.4,-10.8), D (-26.4,-1.2)

From there there are many ways to find the area of the parallelogram. I doubled the area of the top triangle (base 24, height 4.8) and doubled the area of the side triangle (base 12, width 14.4) and added those to the area of the blue rectangle to get 576. (I know there are slicker methods than this.)

I'd be very interested to see a geometric proof that would allow us to bypass the analytic geometry.

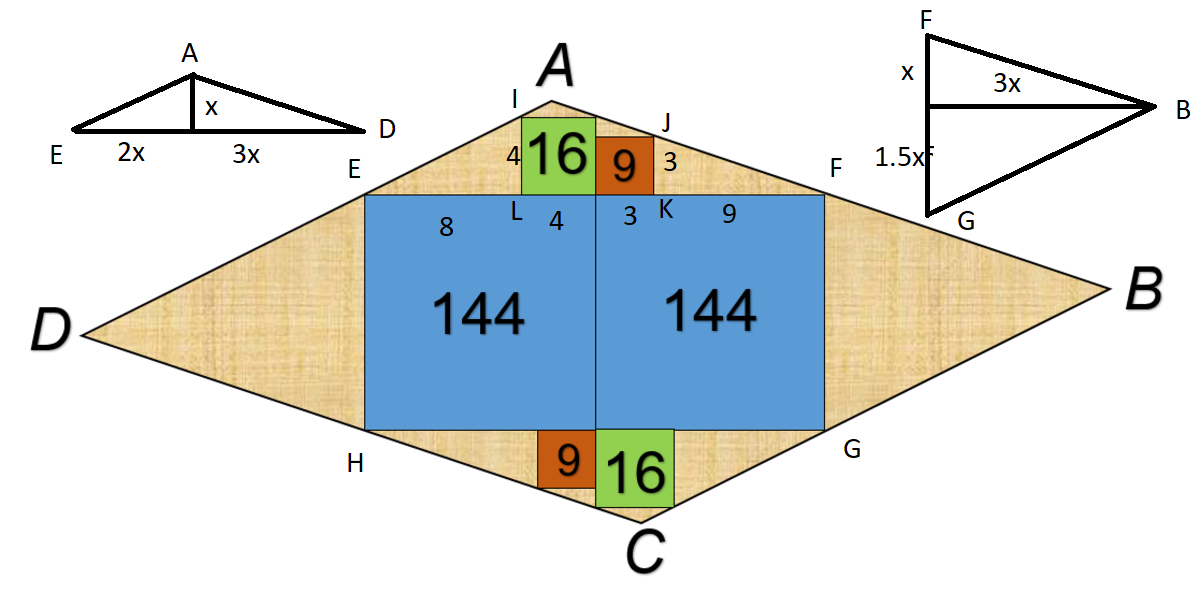You can see in the figure that triangle IEL is a right triangle with hicks 4 and 8. Additionally, you know that triangle JKF is a right triangle with hicks 3 and 9. Therefore, As you can see in the figure, the triangle AEF is composed by two adjacent right triangles similar to IEL and JKF, whose is height. Now we know that $b_{AEF}$ is the base of triangle AEF, $h_{AEF} = x$ his height, and $A_{AEF}$ is its area.

(1) $b_{AEF} = 2x + 3x = 5x = 24 \Rightarrow h_{AEF} = x = \frac{24}{5}$

(2) $A_{AEF} = \frac{b_{AEF} \times h_{AEF}}{2} = \frac{24\times24}{2\times5} = \frac{288}{5}$

Let's (3) $A_{CGH} = A_{AEF} = \frac{288}{5}$ to be the area of triangle CGH.

Finally we have the triangle BFG whose base $b_{BFG}$ is vertical and its height $h_{BFG} = 3x$ is horizontal

(4) $b_{BFG} = x + 1.5x = 2.5x = 12 \Rightarrow x = \frac{24}{5} \Rightarrow h_{BFG} = 3x = \frac{72}{5}$

Let's $A_{BFG}$ and $A_{DEH}$ be the area of the triangles of the triangle BFG and DEH

(5) $A_{BFG} = A_{DEH} = b_{BFG} \times \frac{h_{BFG}}{2} = \frac{12 \times 72}{2 \times 5} = \frac{432}{5}$

Let's A to be the area of the parallelogram ABCD

(6) $A = 288 + 2\times\frac{288}{5} + 2\times\frac{432}{5} = \boxed{576}$