Quadrilateral In Triangle
In a triangle A B C , points D and E are on B C such that ∣ B D ∣ : ∣ D E ∣ : ∣ E C ∣ = 1 : 1 : 1 , and points F and G are on A C such that ∣ A F ∣ : ∣ F G ∣ : ∣ G C ∣ = 1 : 3 : 1 .
The quadrilateral P Q R S is formed by the intersection of segments B F , B G , A D and A E .
If the area of the triangle A B C is 1001 square units, what is the area of quadrilateral P Q R S ?
The answer is 225.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
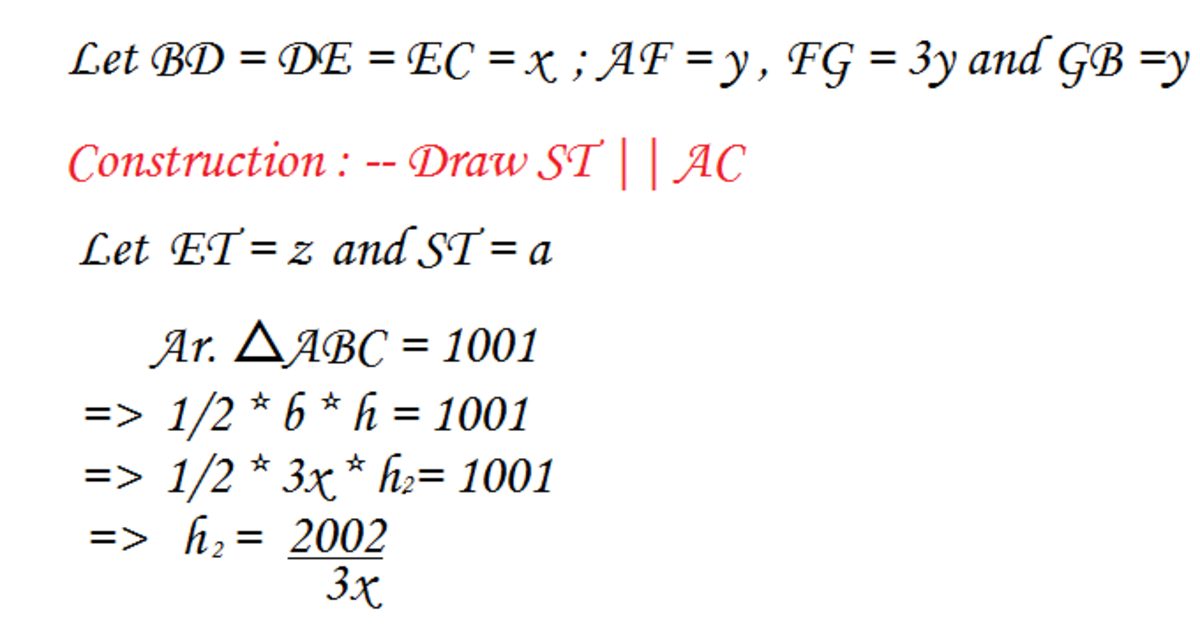


please ask if there is any confusion some steps have been escaped
Completely wrong
Log in to reply
Hmmmmm! Seems like you have got your f e e t r e a l l y w e t in geometry. Go and prove the Thales' theorem to be wrong instead of criticising me here. You guys just write anything here to tarnish other's reputation just because you c o u l d n o t solve it. Its okay! I can understand that was out of f r u s t a t i o n .
Let's define the following vectors:
a = B C
b = B A
B G = u 1 = a + 5 1 ( b − a ) = 5 4 a + 5 1 b
B F = u 2 = a + 5 4 ( b − a ) = 5 1 a + 5 4 b
and
v 1 = 3 1 a − b
v 2 = 3 2 a − b
Each of the points P , Q , R and S corresponds to certain multiples of the vectors that intersect at it.
- Point P: Intersecting vectors v 1 , and u 2
We can write the following vector equation in t and s
t u 2 = b + s v 1
This translates into
t 5 1 a + 5 4 b ) = b + s ( 3 1 a − b )
which implies
t / 5 = s / 3 and 4 t / 5 = 1 − s , for which the solution is
s 1 = 7 3
t 1 = 7 5
2: Point Q. Intersecting vectors: u 1 and v 1
t u 1 = b + s v 1
As before, this translates to:
t ( 5 4 a + 5 1 b ) = b + s ( 3 1 a − b )
which translates into,
4 t / 5 = s / 3
t / 5 = 1 − s
from which,
s 2 = 1 3 1 2
t 2 = 4 5 ( 1 3 4 ) = 1 3 5
3: Point R. Intersecting vectors: u 1 and v 2
t u 1 = b + s v 2
The vector equation translates into,
t ( 5 4 a + 5 1 b ) = b + s ( 3 2 a − b )
which implies,
4 / 5 t = 2 / 3 s
t / 5 = 1 − s
which has the solution:
s 3 = 7 6
t 3 = 7 5
- Point S. Intersecting vectors: u 2 and v 2
Here, the vector equation is:
t u 2 = b + s v 2
This translates to:
t ( 5 1 a + 5 4 b ) = b + s ( 3 2 a − b )
From which we generate two scalar equations:
t / 5 = 2 / 3 s
4 / 5 t = 1 − s
The solution of which is:
s 4 = 1 1 3
t 4 = 1 1 1 0
Now comes the fun stuff !!
Note that the area of middle triangle = [ A D E ] = 3 1 [ A B C ] (why ?)
In addition,
[ A P S ] = s 1 s 4 [ A D E ]
[ A Q R ] = s 2 s 3 [ A D E ]
and
[PQRS] = [AQR] - [APS]
This implies that,
[ P Q R S ] = 3 1 ( s 2 s 3 − s 1 s 4 ) [ A B C ] = 3 1 ( ( 1 3 1 2 ) ( 7 6 ) − ( 7 3 ) ( 1 1 3 ) ) [ A B C ] = 1 0 0 1 2 2 5 [ A B C ]
Since [ A B C ] = 1 0 0 1 , then [ P Q R S ] = 2 2 5 .
Note that we can verify this result, by using the t values that we obtained. We have
[ B F G ] = 5 3 [ A B C ]
In addition,
[ B P Q ] = t 1 t 2 [ B F G ]
[ B R S ] = t 3 t 4 [ B F G ]
and
[ P Q R S ] = [ B R S ] − [ B P Q ]
Therefore,
[ P Q R S ] = 5 3 ( t 3 t 4 − t 1 t 2 ) [ A B C ] = 5 3 ( ( 7 5 ) ( 1 1 1 0 ) − ( 7 5 ) ( 1 3 5 ) ) [ A B C ] = 1 0 0 1 2 2 5 [ A B C ]
Which confirms our previous result.
Another solution using synthetic geometry:
Apply Menelaus' theorem on △ A D C with lines B Q G and B P F as transversals. Apply Menelaus' theorem on △ A E C with lines B R G and B S F as transversals. Through this, one may obtain the ratios
Q A Q D , P A P Q , S A S R , R A R E Then one can very easily find the area of the quadrilateral by expressing it as the [ A Q R ] − [ A P S ] , both of each can be obtained by using the ratios and applying them on the known area of [ A D E ] .
Phenomenal !!
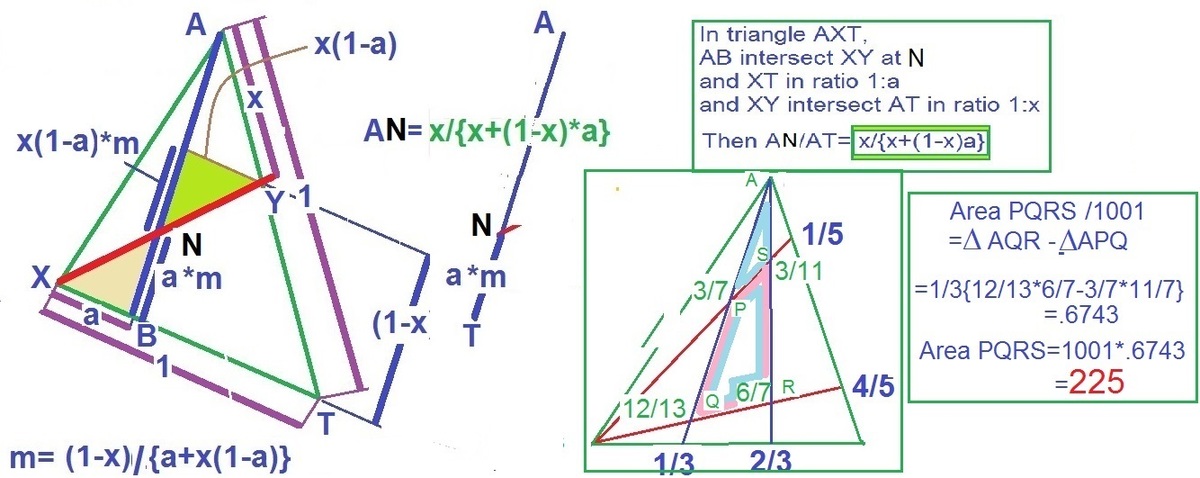
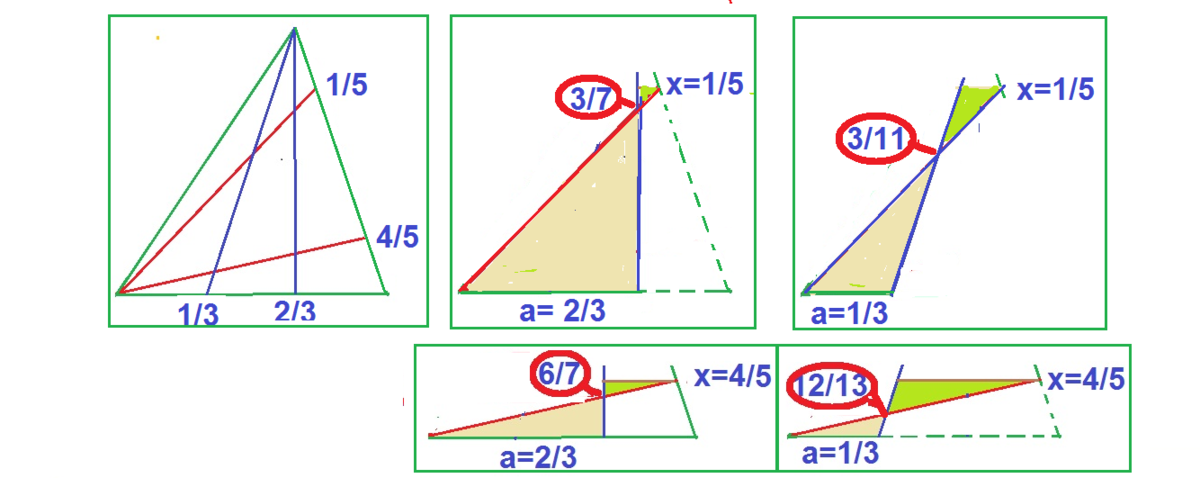
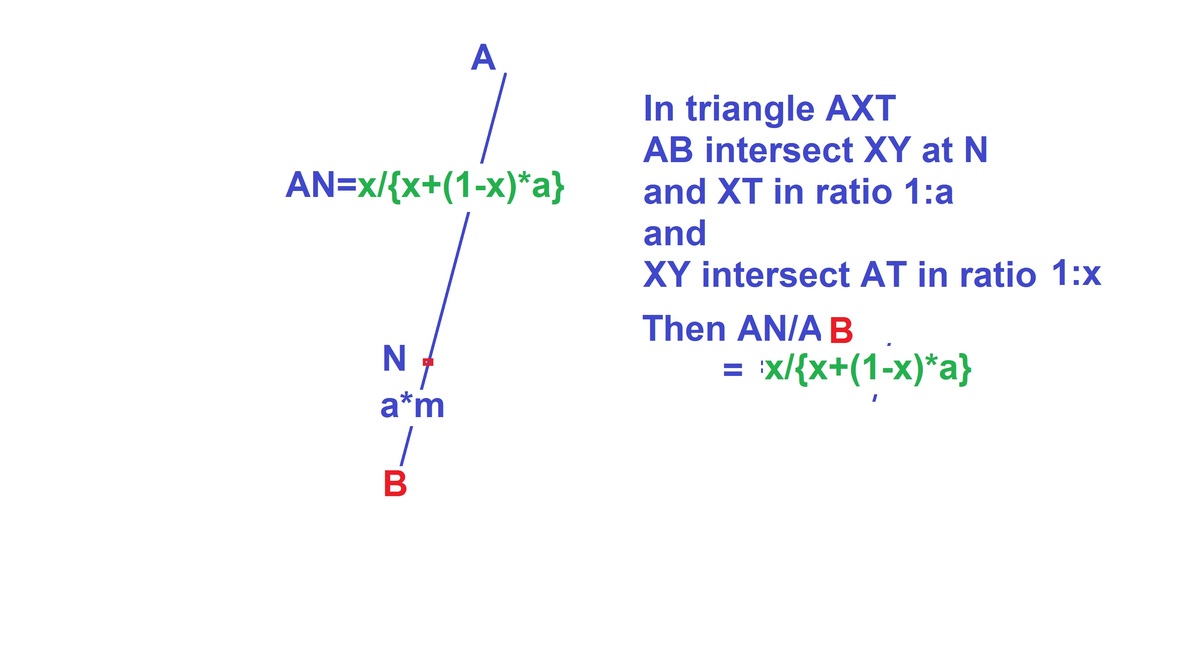
Top left Fig proves the formula
X
+
(
1
−
X
)
a
X
how two intersecting lines from vertices to opposite sides are divided.
Bottom five sketches apply this to the given problem.
Top right Fig. leads us to the answer. Please correct the word box and fig for a mistake. Replace T with red B as shown in the bottom most Fig.