Area of Row
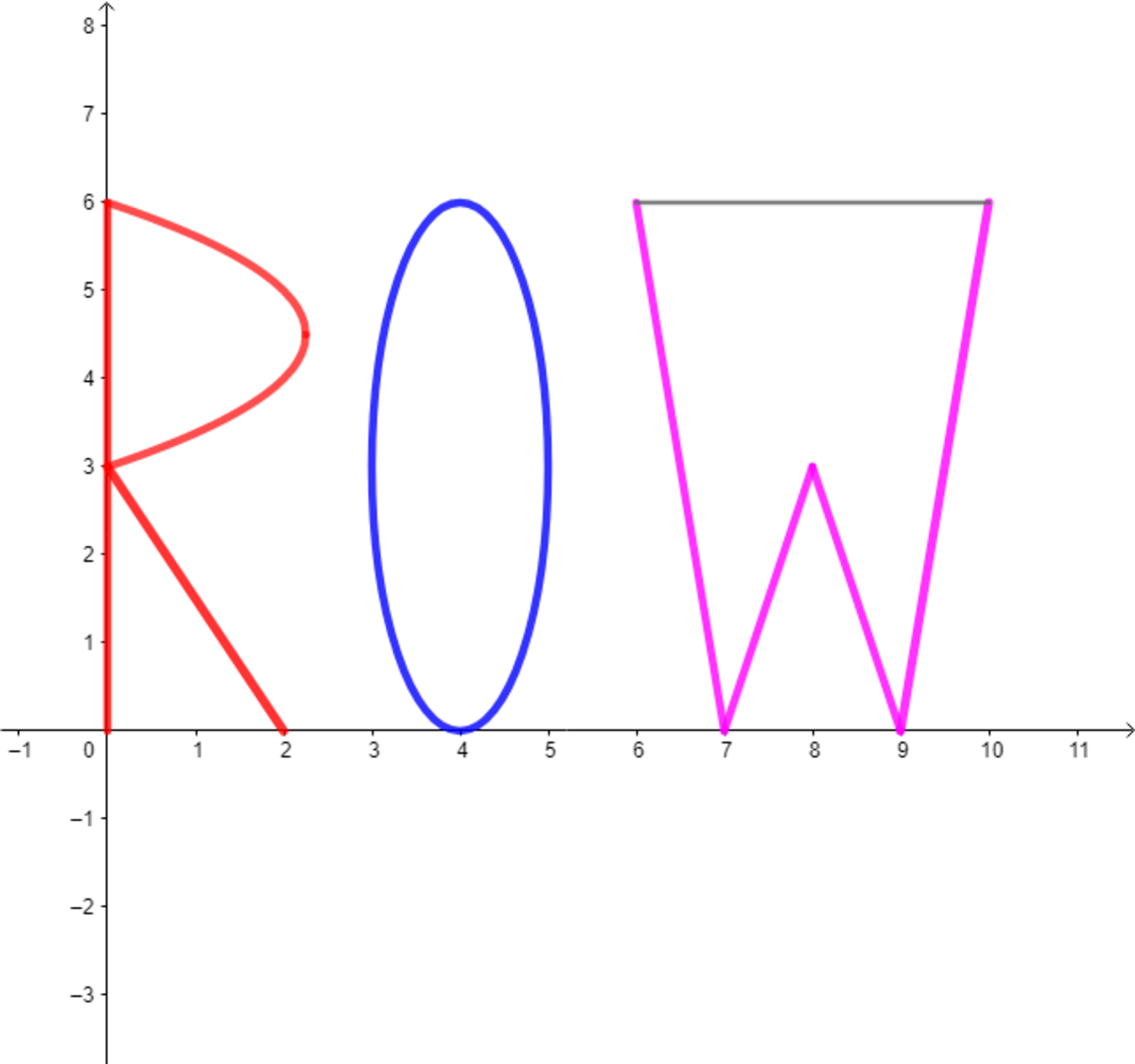
The letter is composed of the following curves:
The region bounded by and the positive axis from to .
The region bounded by , and .
The letter is the region of the ellipse .
For the letter with the line , reflect the lines from to and from to about the line forming the desired bounded region..
Find the Area of . That is, find the sum of the areas to six decimal places.
The answer is 43.924777.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the letter R above:
A R = − ∫ 3 6 y 2 − 9 y + 1 8 d y + 3 = − ( 3 y 3 − 2 9 y 2 + 1 8 y ) ∣ 3 6 + 3 = 3 + 2 9 = 2 1 5 .
For the letter O using the ellipse above:
A e = 6 ∫ 3 5 1 − ( x − 4 ) 2 + 1 d x
Let x − 4 − sin ( θ ) ⟹ d x = cos ( θ ) d θ ⟹ A e = 6 ( 2 1 ( θ + 2 1 sin ( 2 θ ) ) ∣ 2 − π 2 π + x ∣ 3 5 ) = 3 ( π + 4 )
For the letter W with the line y = 6 :
Using the symmetry about the line x = 8 :
On the left side of the line x = 8 we have a right triangle and a trapezoid ⟹ A W = 2 ( 3 + 2 9 ) = 1 5
∴ The sum of the areas A R O W = 2 6 π + 6 9 ≈ 4 3 . 9 2 4 7 7 7 .
Note: Using the definite integral for the letter W with the line y = 6 we obtain:
Again, using the symmetry about the line x = 8 ⟹ A W = 2 ( ∫ 0 6 3 y + 2 1 − ( 6 4 2 − y ) d y − ∫ 3 6 8 − ( 3 y + 2 1 ) d y ) =
2 ( 4 1 y 2 ∣ 0 6 − 3 1 ( 3 y − 2 y 2 ) ∣ 3 6 = 2 ( 9 − 2 3 ) = 1 5 .