Area of shaded part
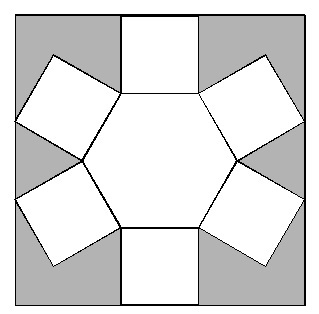 The length of each side of the regular hexagon above is
. It is surrounded by six squares. The six squares are enclosed by another square. Find the area of the shaded part.
The length of each side of the regular hexagon above is
. It is surrounded by six squares. The six squares are enclosed by another square. Find the area of the shaded part.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Now, we need to compute for the area of the six squares, and that is 6 ( 6 2 ) = 6 ( 3 6 ) = 2 1 6 .
We also need to calculate the area of the regular hexagon. A regular hexagon is composed of 6 equilateral triangles. All we have to do is to get the area of one regular hexagon then multiply it by six. We can used the derived formula A = 4 3 x 2 where x is the side length of the equilateral triangle. So the area of the regular hexagon is 6 ( 4 3 ) ( 6 2 ) = 5 4 3 .
Now to get the area of the shaded part, we simply subtract the areas of the six small squares and regular hexagon from the the area of the big square. We have
2 5 2 + 1 4 4 3 − 5 4 3 − 2 1 6 = 3 6 + 9 0 3