This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
100% correct.
Log in to reply
Thanks. Nice problem. +1
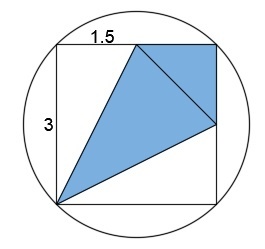 The diagonal of the square is also the diameter of the circle. The diagonal of the square is given by
d
=
x
2
. Substituting, we get
The diagonal of the square is also the diameter of the circle. The diagonal of the square is given by
d
=
x
2
. Substituting, we get
3 2 = x 2
x = 3
So A E = 2 3 = 1 . 5 .
The unshaded part inside the square is a 3 × 1 . 5 rectangle. The area of the shaded part is equal to the area of the square minus the area of the unshaded part.
3 2 − ( 3 × 1 . 5 ) = 9 − 4 . 5 = 4 . 5
Let the side length of the square be x
By Pythagoras, x 2 + x 2 = ( 3 2 ) 2 = 1 8 , therefore x = 3
Square Area = Shaded Area + Non-shaded Area
⟹ Shaded Area = Square Area - Non-shaded Area
= 9 − △ A E D − △ C F D
= 9 − 2 . 2 5 − 2 . 2 5 = 4 . 5
Nice solution.
Since the radius is equal to 2 3 2 , we can deduce that the side length of the square is 3. So the area of the shaded region equals the area of the square minus the area of the two right triangles not shaded. The area of the square is obvious 9, and we can easily find both triangles' areas: 2 3 ⋅ 3 = 2 9 . And 9 − 2 9 = 2 9 = 4 . 5 .