Area of shaded region between three circles and a boundary
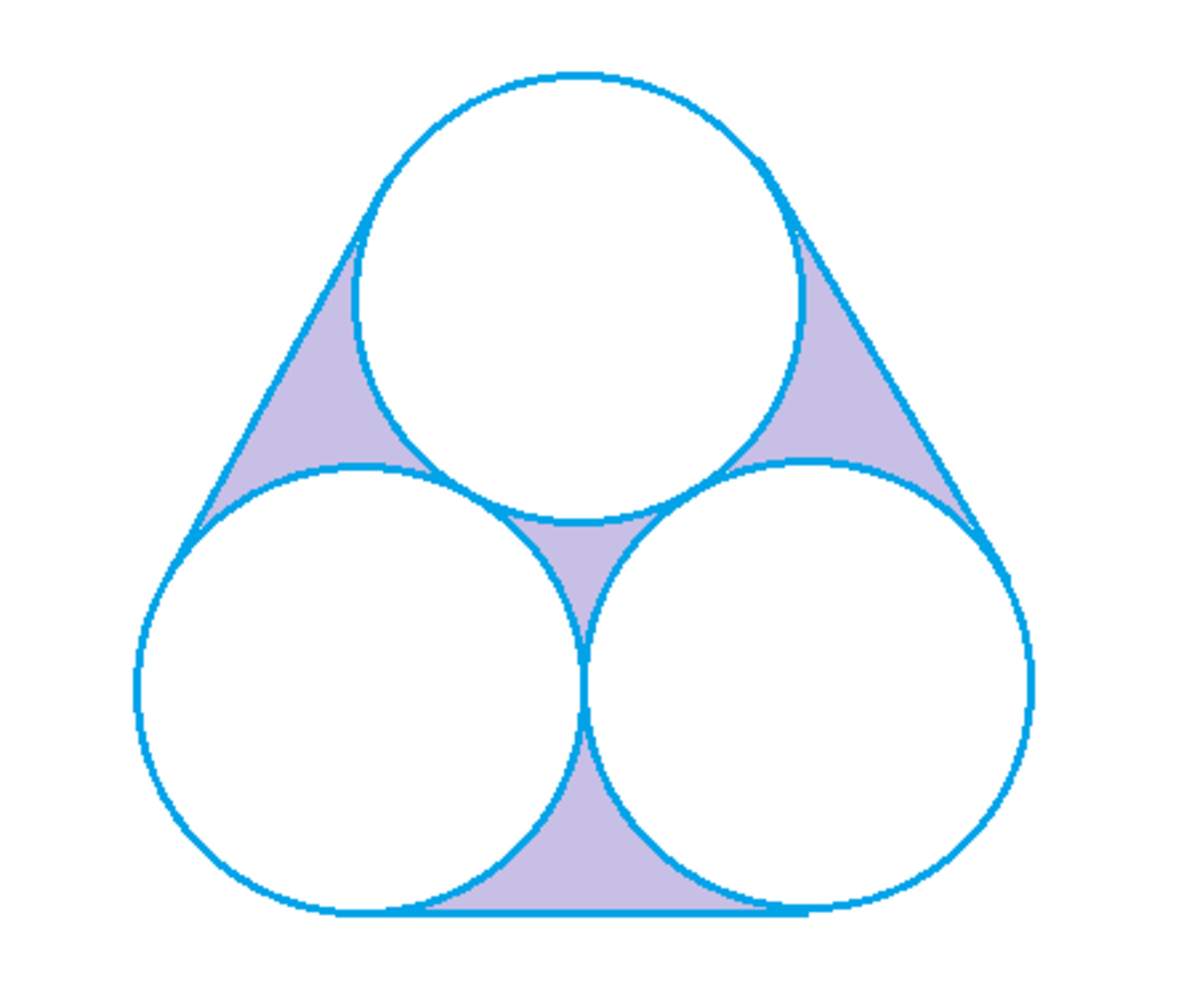
Three unit circles are tangent to each other, as shown in the figure above. Find the area of the shaded region. If the area can be written as for positive integers , , and , find .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Extend the sides to make an equilateral triangle, and label it as follows:
Since A B = A C = 1 and ∠ B A C = 6 0 ° , C Q = D R = 3 , the area of △ A Q C is A △ A Q C = 2 3 , the area of sector A B C is A A B C = 6 1 π , and the area of the blue region bounded by B C Q is A B C Q = A △ A Q C − A A B C = 2 3 − 6 1 π .
Since R Q = R D + D C + C Q = 3 + 2 + 3 = 2 + 2 3 , the area of equilateral △ P Q R is A △ P Q R = 4 3 ( 2 + 2 3 ) 2 = 6 + 4 3 .
The area of the purple region is then A purple = A △ P Q R − 3 A circle − 6 A B C Q = ( 6 + 4 3 ) − 3 π − 6 ( 2 3 − 6 1 π ) = 6 + 3 − 2 π .
Therefore, a = 6 , b = 3 , c = 2 , and a + b + c = 1 1 .