Area of shaded region problem

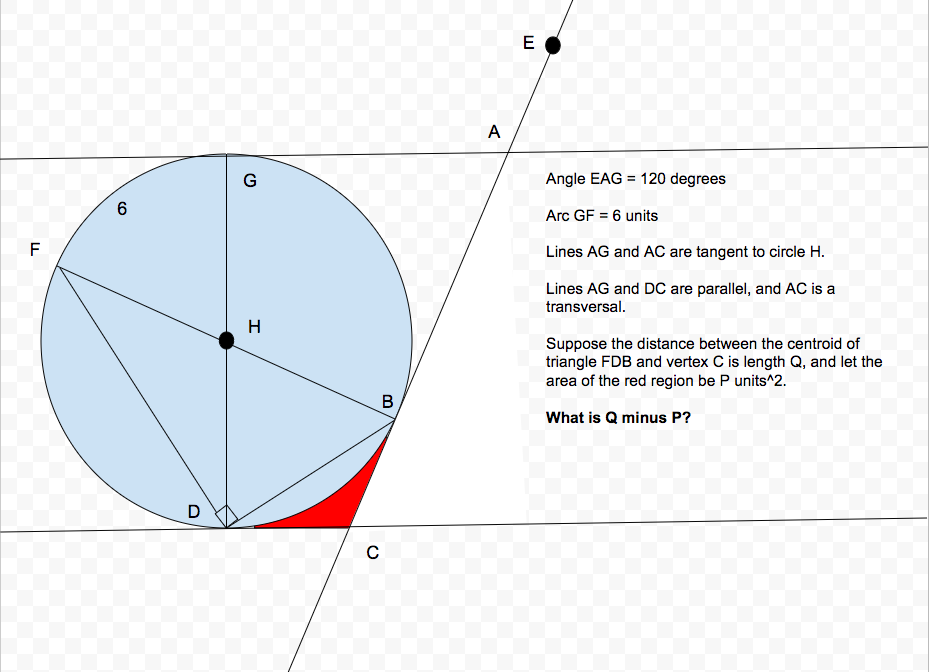
Since AD and DC are parallel, angle BCD = 120 degrees. Angle GAB = 180-120 = 60 degrees. Since AB and AG are tangents, then the angles HGA and HBA both equal 90 degrees. Since GHBA is a quadrilateral, its angles sum up to 360 degrees. As a result, angle GHB = 360-90-90-60, which equals 120. Angle GHF = 180-120=60 degrees. Since GHF is 60 degrees, and 60 degrees is 1/6 of a 360-degree rotation, and the arc angle GHF subtends (arc FG) has a length of 6 units, we multiply the length of arc FG by 6 so we get the full circumference of 36 ( 60 / 360 = 6 / c, where c is the circumference, so 60c / 360 = 6, 60c = 3606 = 2160, 60c=2160, c=2160/60 = 36). Since the formula for circumference is πd = c, where d is the diameter, and we know the circumference is 36, then πd=36, d=36/π = 11.46. Since the GHF and BHD are vertical, they are congruent. Since angle GHF = 60 degrees, so does angle BHD. Since BH and HD are congruent, triangle DBH is isosceles. In turn, the angles HBD and HDB are also congruent. We can set up an algebra equation to find what angles HBD and HDB are; 2x+60=180, where x is the measure of HBD and HDB. By simplification, x=60. We see that triangle DBH is equilateral. Since line CB is tangent to the circle, angle HBC = 90 degrees. We also know that HBD = 60 degrees. As a result, angle DBC = 90-60 = 30 degrees. Since CB and CD are both tangent to the circle, CB=CD, so triangle DCB is isosceles. In turn, angle BDC is also 30 degrees (or: 180-30-120 = 30). To find the area of triangle DCB, we can use Heron's Formula. We could have used 1/2 * base * height, but it is probably impossible to decode the length of an altitude from vertex B down to line DC, and the length from vertex C to where the altitude makes a right angle with line DC. We know the length of BD is the radius of the circle (since triangle DBH is equilateral), and the radius is equal to 1/2 * 36/π = 36/2π = 5.73. We can use the Law of Sines to decipher what CB and CD would be. Consequently, sin(120) / DB = sin(30) / BC (you could also do sin(30) / DC, they are the same thing). Since DB = 5.73, then sin(120) / 5.73 = sin(30) / BC. Furthurmore, (sqrt(3)/2) / 5.73 = (1/2) / BC, and we find that BC = 3.3, which also equal DC. Heron's Formula states that if we have a triangle ABC, then S = )AB + BC + AC) / 2, the sqrt ( S (S-A) (S-B) (S-C) ). We can substitute to see that S=(3.3+3.3+5.73) / 2 = 6.165. Subsequently, the area of triangle DCB is: sqrt ( 6.165 (6.165-3.3) (6.165-3.3) (6.165-5.73) ) = 4.69. We have to now find the area of the red region. Because the angles FHG and BHD are vertical and angle FHG = 60 degrees, then angle BHD is also 60 degrees. The area of the circle is πr^2, where r is the radius, which equals π(5.73)^2 = 103. Since BHD = 60 degrees, which is 1/6 of a full rotation, the area of the sector made by angle BHD is 1/6 of the whole area of the circle, which equals 103/6 = 17.167. Now, to find the area of the red region, first, subtract the area of triangle DHB from the area of the sector made by angle BHD to find the area of the region made by line segment BD and arc BD. To find the area of triangle BHD, draw an altitude from point H to side DB. We can call the point where the altitude intersects with DB point L. This divides triangle DHB into 2 congruent right triangles (use AAS congruence to prove it to yourself if you are skeptical of that) - triangles LBH and LDH. Since the 2 right triangles are congruent, LB = LD, so any of them would be BD/2, which is 5.73/2 = 2.865. Use the Pythagorean Theorem to find the altitude: (DH)^2 = (LH)^2 +(LD)^2 (you could also do (BH)^2 = (LH)^2 + (LB)^2, it is the same thing). We can substitute for LH and DH to find: (LH)^2 + (2.865)^2 = (5.73)^2, or LH = sqrt( (5.73)^2 - (2.865)^2 ) = 4.96. Now that we have a base and height of triangle DBH, we can apply 1/2 * base * height for the area: 1/2 * (4.96) * (5.73) = 14.21. Finally, we can subtract this value from the ara of the sector made by angle BDH. 17.167-14.21 = 2.957. This is the area of the region made by line segment BD and arc BD. To find the area of the red region, subtract 2.957 from the area of triangle ABC to get: 4.69 - 2.957 = 1.733 units^2. This value is P. To find Q, we have to know that since HB and HF are both radii, they are congruent. As a result, point H is the midpoint BF, which is the hypotenuse of triangle FDB. Also, line DH is the median of triangle FDB since it is a bisector of side FB and intersects angle FDB. Since the centroid of any triangle is 2/3 along the median, and we have figured out that DH (which is a median) = 5.73, (2/3)5.73 = 3.82. Suppose point N marked the centroid of triangle FDB, so ND=3.82. Since HD is a radius and CD is tangent to the circle, HDC is a right angle. We can think of ND as a height and NC as a hypotenuse, and we know what ND and DC are, so we can use the Pythagorean Theorem to find the value of NC. (ND)^2 + (DC)^2 = (NC)^2, so (3.82)^2 + (3.3)^2 = (NC)^2, and we can simplify this to figure out that NC equals around 5 units. This value is Q. Since the problem asks for Q-P, and P=1.733 and Q=5, then 5 - 1.733 gives us a final answer of* 3.267* units.