Area of Shapes - 1
The following picture has been given to you.
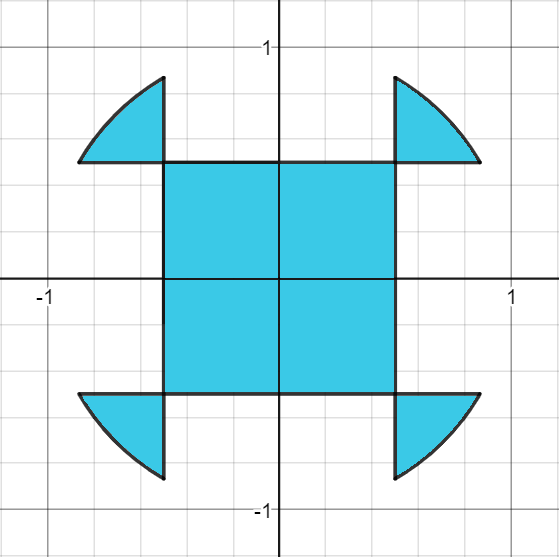 Calculate the area marked in blue.
Calculate the area marked in blue.
Details:
-
The curved parts at the sides of the shape are part of the circle given by the formula x 2 + y 2 = 1 .
-
The vertical lines in the shape are given by the lines x = 2 1 and x = − 2 1 .
-
The horizontal lines in the shape are given by the lines y = 2 1 and y = − 2 1 .
The following picture might be of help.
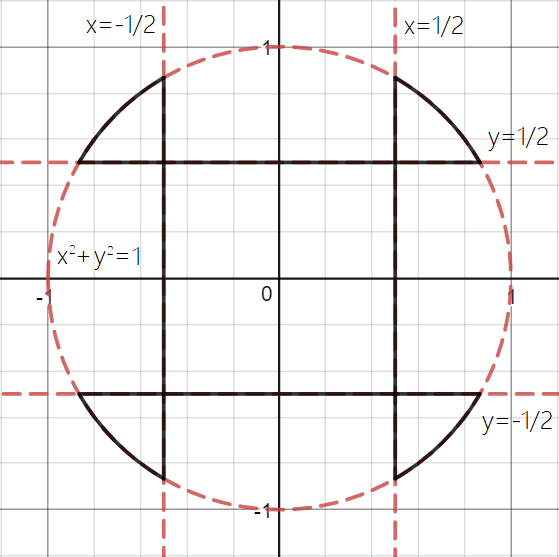
The answer is 1.31514674363.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice simple solution, Sir Otto!!
We know that the circle in total has an area of π ⋅ 1 2 = π . We notice that this shape misses only four parts of the circle. Moreover, those four parts can be split in 2 each and those are of equal size, because of the symmetry within the picture. One can notice that the area of one of those parts equals ∫ 0 2 1 ( 1 − x 2 − 2 1 ) d x To calculate this integral, we make use of the substitution x = sin ( u ) . It follows that d x = cos ( u ) d u and thus, ∫ 0 2 1 ( 1 − x 2 − 2 1 ) d x = ∫ 0 6 π ( 1 − sin 2 ( u ) − 2 1 ) ⋅ cos ( u ) d u = ∫ 0 6 π ( cos 2 ( u ) − 2 cos ( u ) ) d u Using the double angle formula for cos ( 2 u ) to our advantage, we get that cos 2 ( u ) = 2 cos ( 2 u ) + 1 . Now it follows that ∫ 0 6 π ( cos 2 ( u ) − 2 cos ( u ) ) d u = ∫ 0 6 π ( 2 cos ( 2 u ) + 1 − 2 cos ( u ) ) d u = 4 sin ( 2 u ) − 2 sin ( u ) + 2 u ∣ ∣ ∣ ∣ ∣ u = 0 u = 6 π Furthermore, we know that 4 sin ( 2 u ) − 2 sin ( u ) + 2 u ∣ ∣ ∣ ∣ u = 0 u = 6 π = 4 sin ( 3 π ) − 2 sin ( 6 π ) + 1 2 π − 0 = 8 3 − 4 1 + 1 2 π At last, we remember that this value equals the area of one out of eight missing parts of the shape to be a full circle with area π . So, the area asked in the problem equals π − 8 ⋅ ( 8 3 − 4 1 + 1 2 π ) = π − 3 + 2 − 3 2 π = 2 + 3 π − 3
We can do this using simple geometry; no calculus required. The area A of the "missing piece" on top (bounded by the lines y = 2 1 , x = 2 1 , x = − 2 1 and the circle) is the area of a sector of 6 0 o plus two triangles of area 2 1 2 1 2 3 each minus the area of a rectangle of area 1 × 2 1 . In summary, A = 6 π + 4 3 − 2 1 . The area we seek is π − 4 A = 3 π − 3 + 2 ≈ 1 . 3 1 5 .