Area of Shapes - 2
You might want to take a look at this problem first. Take a look at the following picture.
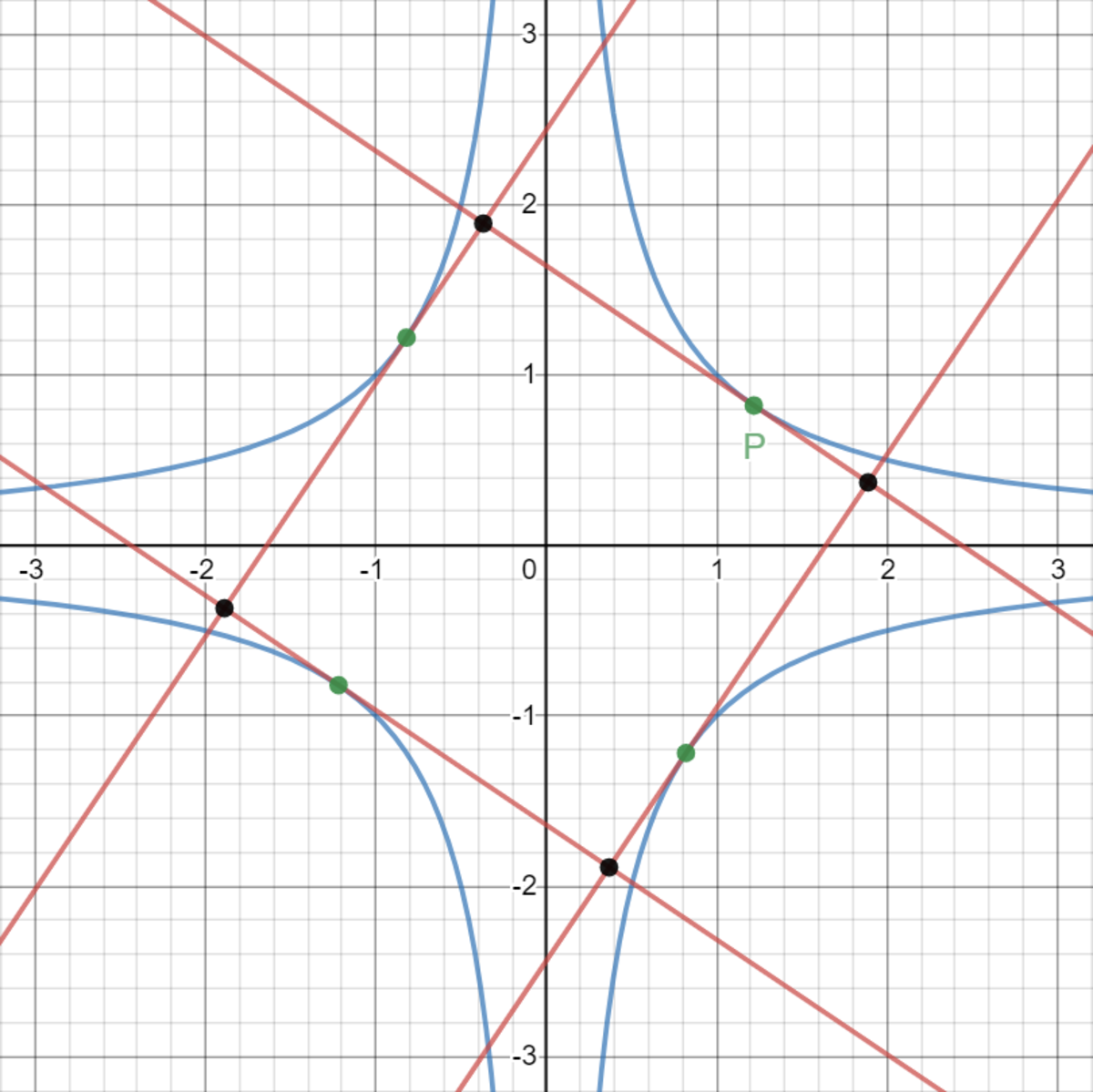
In this picture you can see the graph of the curve (colored blue) in the Cartesian plane. In this picture, is a point on the curve in the first quadrant. In the picture there is drawn a red line touching the curve at . There are also drawn two other red lines perpendicular to it, such that they touch the curve as well (at different points, colored green). There is one last red line perpendicular to the two red lines before, such that it touches the curve as well, again. Finally, the intersections of the red lines are given by black dots.
If we change the position of , we will always get black dots, but those will be at different positions. Calculate the area bounded by the curve that consists of the collection of those black dots.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To prepare ourselves for polar integration, we want to choose P in terms of radians. Let P = ( cot ( θ ) , tan ( θ ) ) . By doing this, P is the point at an angle + θ radians from the positive x -axis, located at the blue curve. (This can be done by substituting y = tan ( θ ) x in the equation for the blue curve.)
Let now t = cot ( θ ) . The tangent to the curve at the point P can be written as y = t 2 t − x + t 1 = t 2 2 t − x . We want to find the perpendicular line to this tangent touching the curve in the fourth quadrant. We can do this, using the fact that the product of the slopes must be equal to − 1 . So, the slope of the perpendicular line is equal to t 2 and so we can find that the perpendicular line has the form y = t 2 ( x − t 1 ) − t = t 2 x − 2 t .
Now, we will find the intersections of the two tangents. Notice that for the intersection t 2 2 t − x = t 2 x − 2 t , and so 2 t − x = t 4 x − 2 t 3 , from which follows that x = t 4 + 1 2 t ( t 2 + 1 ) . By plugging in this value for x in one of the equations of the tangents, we find that y = t 4 + 1 2 t ( t 2 − 1 ) .
We now want to find the area enclosed by the orange curve, which is, by symmetry and the polar integration equation, equal to A : = 8 ⋅ 2 1 ⋅ ∫ 0 4 π r 2 ( t ) d θ , where r 2 ( t ) is the squared length of the point ( x ( t ) , y ( t ) ) = ( t 4 + 1 2 t ( t 2 + 1 ) , t 4 + 1 2 t ( t 2 − 1 ) ) . Some calculations will lead to the conclusion that r 2 ( t ) = t 4 + 1 8 t 2 . Knowing that t = cot ( θ ) , we notice that A = 4 ⋅ ∫ 0 4 π cot 2 ( θ ) + 1 8 ∣ cot ( θ ) ∣ d θ = 3 2 ⋅ ∫ 0 4 π csc 2 ( θ ) cot ( θ ) d θ = 3 2 ⋅ ∫ 0 4 π sin ( θ ) cos ( θ ) d θ = 1 6 ∫ 0 4 π sin ( 2 θ ) d θ = − 8 cos ( 2 θ ) ∣ ∣ ∣ ∣ 0 4 π = 8 .
Edit: The shape of the collection of black dots looks like the following orange curve.