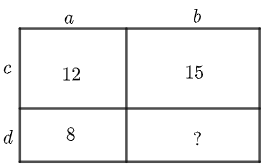
Area of the fourth rectangle?
The numbers in the rectangles represent their respective areas.
What is the area of the fourth rectangle?
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Thank you for sharing your solution.
I don't understand. Why must the ratio be consistent?
Log in to reply
Because the ratio of the areas of any two squares of the same width is equal to the ratios of their heights.
According to Geoff's equation: multiply x on both sides. This should give you 12x/8 = 15. Divide 12 by 8 and you answer is 1.5x = 15, when you divide 15 by 1.5 your answer will be 10 thus x = 10
Nice, very clean and simple way of looking at the problem
Thanks, now yes !! Simple and easy
ug im so bad i still have no idea why you would use a ratio!
I just tried to find a common divisor for 12 and 15, and that gave me 3, so the other sides got solved alone
Are you SURE you couldn't make this a system of 8 nonlinear equations with 7 unknowns and solve by perturbation theory?
Hanna -- Do you work in a math-related occupation ?
Log in to reply
Yes, I do.
Why is "ac x bd = abcd"? And what is "abcd"?
I still don't really understand
Label the sides of the rectangle as follows:
 Then we know the following:
a
c
a
d
b
c
=
1
2
=
8
=
1
5
Then
c
=
a
1
2
, which in turn implies that
b
=
c
1
5
=
1
2
1
5
a
=
4
5
a
. Additionally,
d
=
a
8
. Thus, the unknown area is
b
d
=
4
5
a
×
a
8
=
1
0
Then we know the following:
a
c
a
d
b
c
=
1
2
=
8
=
1
5
Then
c
=
a
1
2
, which in turn implies that
b
=
c
1
5
=
1
2
1
5
a
=
4
5
a
. Additionally,
d
=
a
8
. Thus, the unknown area is
b
d
=
4
5
a
×
a
8
=
1
0
Thank you, neat and logical solution.
There must be some steps missing.
Log in to reply
I don't believe I've skipped anything... the first set of equations follows from the areas of the given rectangles and from there it's just rearranging and substituting. Is there a specific point where you think I've missed something?
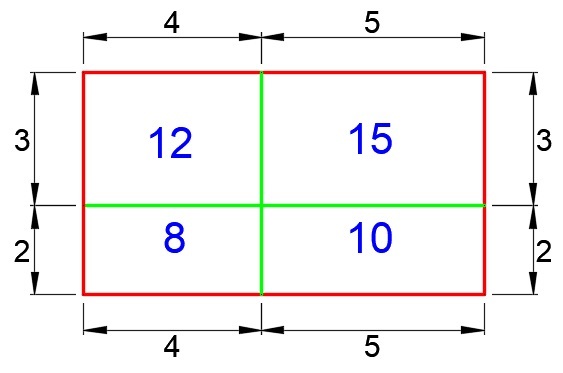 One way of solving this is by putting the dimensions of the rectangles with given areas. Then compute the area of the unknown rectangle.
One way of solving this is by putting the dimensions of the rectangles with given areas. Then compute the area of the unknown rectangle.
Thank you for sharing your solution.
How do you make these type of images.
12=3×4, 15=3×5, 3 is common side to area 12 and 15 therefore 4 is common between 12 and 8 so 8÷4=2 , 2 is common side with X. 5 is the other side of area 15 and must be common to X so X=2x5=10 with perimitor = (4+5+2+3)×2=28
Thank you for sharing your solution.
This is a problem of proportion. Simply multiply 15 by 8 and divide the product by 12. The answer is 10. Total area of the rectangle is 45.
Nice method.
"Simply" explain that.
3rd rectangular is 2/3 of 1st rectangular. So, 4th rectangular should be 2/3 of 2nd rectangular. Multiplication 2/3*15 = 10. Ans. 10
From inspection we see: “8 is to 12 as x is to 15”; 8/12 = x/15; 2/3 = x/15; 2/3 * 15 = x; x = 30/3; x = 10
We know that to factor we can go two ways, 1 15 or 3 5. Starting with 3*5, we label the larger sides of rectangle 15 5 units and the smaller sides 3 units. Then, since rectangle 12 shares a smaller side with rectangle 15, we know that the smaller sides of 12 are going to be 3. To factor 12 by 3, we get 4, so we label the bigger sides by 4. That makes box 8 share a larger side with the larger side of box 12 (which we just labeled 4). Then we factor 8 by 4 and get 2. That makes the smaller side of the box 2, giving the 2 sides we need to multiply to get the area for the mystery box
15 is only divisible by 3 and 5, hence the longer side is 5. 8 is divisable by 2 and 4. The shorter size being 2. Area is solved by multiplying the length and 2 x 5 is 10.
Yes-simplest way
This is true if the sides are integers, but I don't think the question specifically states that.
I approached the problem like this:
12:15 :: 8:x
Or 12 is to 15 as 8 is to x
So 12/15 = 8/x
Cross multiply to get 12x = 8*15 and Simplify 12x = 120, thus x=10
Thank you for sharing your solution.
Top left is 4x3 top right is 5x3 Bottom left is 4x2, therefore bottom right is 5x2, or 10
Thank you for sharing your solution.
The area of rectangle 1= 12, the area of rectangle 2=15, the area of rectangle 3= 8, so then what is the area of rectangle 4. As we can see, Rectangle one and three have a common side, which is shared by both rectangles. Therefore, the length of that side equals a common factor of the two numbers, 8 and 12. The only three common factors that these two numbers have are (1,2,4). Using the trial and error method, we get that 1 and 2 are not the length of the shared side. Therefore, when we use four, we get that the width of the outer rectangle=5, as 4 3=12, and 4 2=8. 3*5=15, and that is how we know the length of the common side of rectangle 2 and 4. 5, when multiplied by 2, which is the width of rectangle four, as is the width of rectangle three, being the common side between them, gives us 10.
Thank you for sharing your solution.
15×8=12×Unknown area. i.e unknown area=120/12=10
Nice method.
8/4=2 and 15/3=5 and 2*5=10
The sides of the rectangles are common hence there will be a common factor for every 2 adjacent rectangles the relationship can further be deduced .
Consider the side shared by 12 and 8 . Call it A. A must be a common factor of 12 and 8, so either 2 or 4. If it's 2, then the side shared by 12 and 15 would have to be 6. But 6 doesn't divide 15, so A is 4. We can now find the side lengths of the missing rectangle, and thus find its area to be 10.
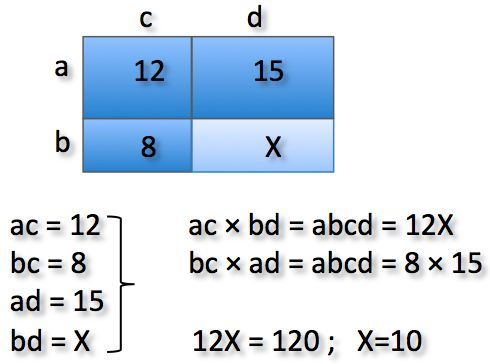
The ratios of the areas on top over the areas on the bottom must be consistent, so 8 1 2 = x 1 5
So, x = 1 0