Area of the green region
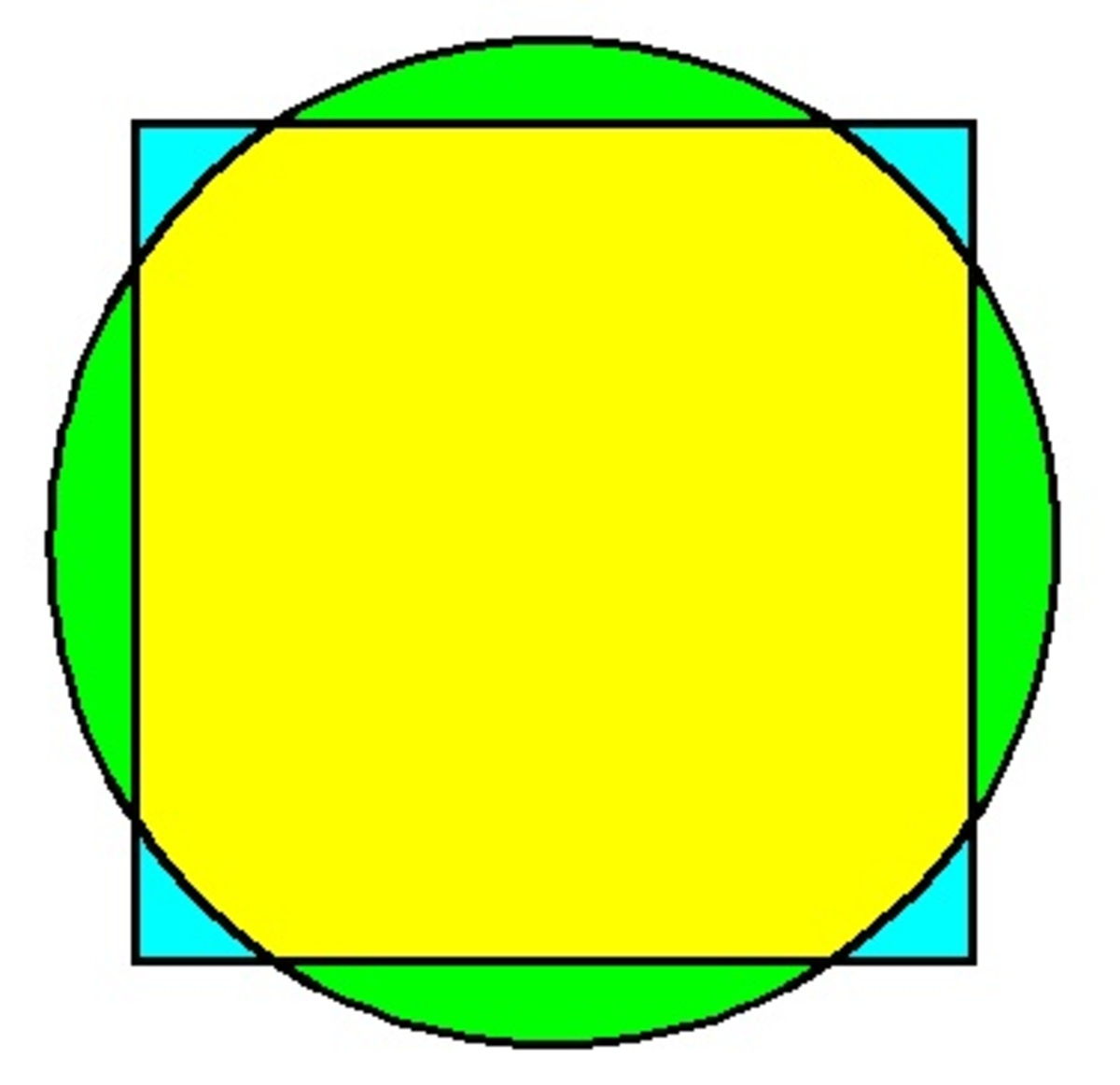 The figure above shows a square with side
and a circle with radius
. The center of the circle coincides with the center of the square. Find the area of the green region in
rounded to the nearest whole number.
The figure above shows a square with side
and a circle with radius
. The center of the circle coincides with the center of the square. Find the area of the green region in
rounded to the nearest whole number.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Solve for the central angle.
c o s ∅ = 2 . 4 2
∅ = 3 3 . 5 6 ; 2 ∅ = 6 7 . 1 2
Solve for the area of the triangle.
By Pythagorean Theorem, x = 2 . 4 2 − 2 2 = 1 . 7 6 ; 2 x = 2 1 . 7 6
A t r i a n g l e = 2 1 ( 2 1 . 7 6 ) ( 2 ) = 2 1 . 7 6
Solve for the area of the sector.
A s e c t o r = 3 6 0 6 7 . 1 2 π ( 2 . 4 2 ) = 3 . 3 7
Solve for the area of the green region.
A g r e e n = 4 ( A s e c t o r − A t r i a n g l e ) = 4 ( 3 . 3 7 − 2 1 . 7 6 ) = 3 s q u a r e m e t e r s