Area of the locus
Let and be circles with centres units apart, with radii of length and respectively. Firstly find the locus of all points for which there exist points on and on such that is the midpoint of the line segment . Then find the area of the closed region inscribed by the locus.
The answer is 9.42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
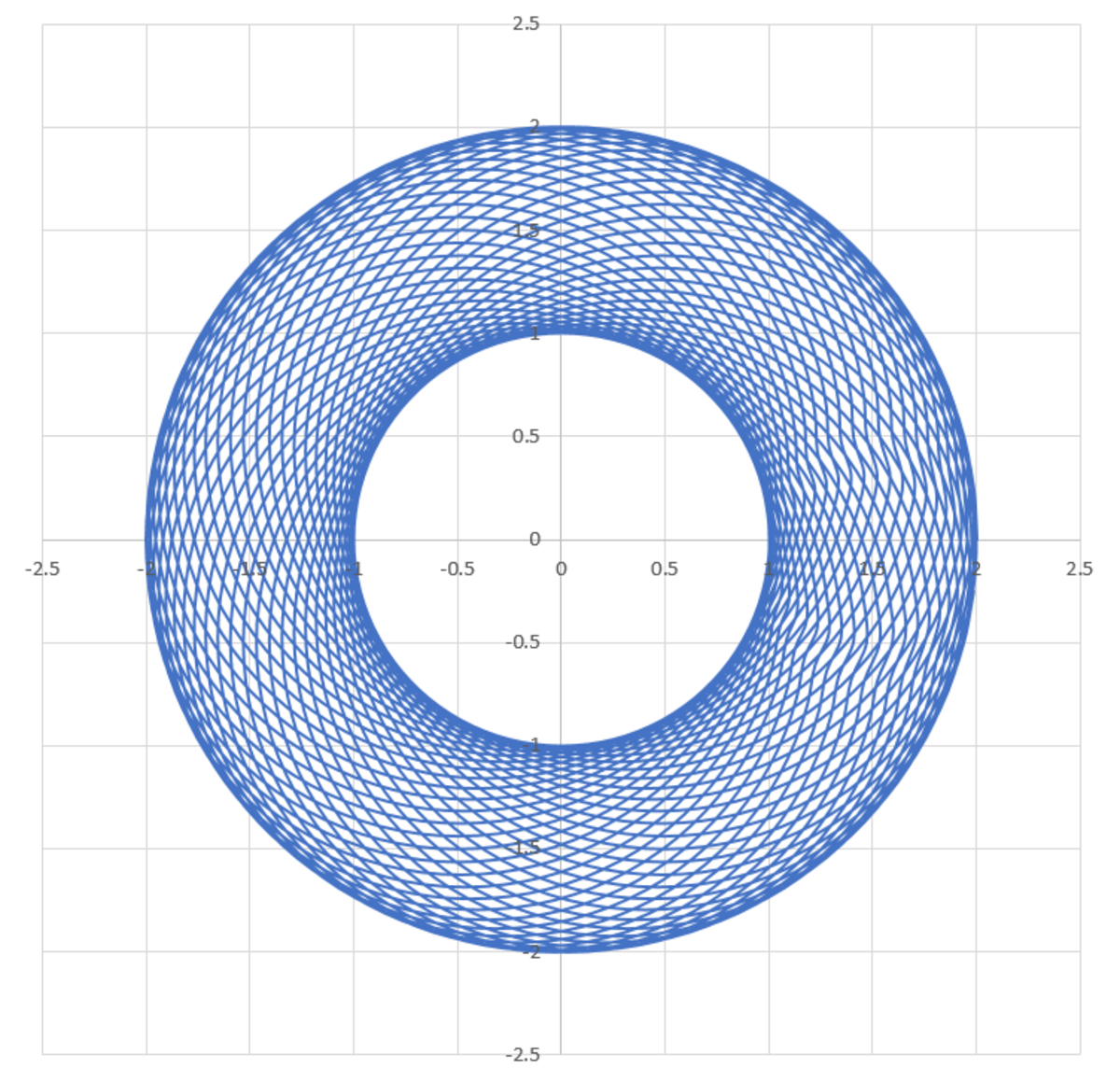
Let X = a + e i α Y = b + 3 e i β
M = 2 X + Y = 2 a + b + 2 e i α + 3 e i β
Now let α and β vary for − π ≤ α , β ≤ π then 2 e i α + 3 e i β is simply a circle of radius 2 1 with its centre on the circumference of a circle with radius 2 3 . So the locus of points is an annulus with inner radius 1 and outer radius 2 .
Area of the annulus is π ( 2 2 − 1 2 ) = 3 π ≈ 9 . 4 2