Area of the Outer Triangle
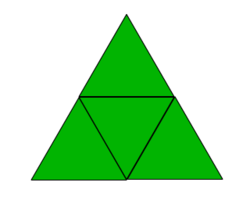All the triangles you see here are equilateral triangles. Since the internal triangles share the sides, therefore they are all congruent too.
If a side of the internal triangle is , what is the area of the outer triangle?
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
AS THE INTERNAL TRIANGLES ARE CONGRUENT AND EQUAL AND EQUILATERAL,SO THE TRIANGLE WITH BLACK OUTLINE HAS SAME LENGTHS,SO ALL THE TRIANGLES IN THE OUTER TRIANGLE HAS THE SAME LENGTHS,THEN THE SIDE OF THE OUTER TRIANGLE IS 2(5/to the power 4 root 3)=10/Tto the power 4 root 3,THAT MAKES THE AREA OF THE OUTER TRIANGLE IS (sqr root 3/4) (10/to the power 4 root 3)^2=(sqr root 3/4) (100/sqr root 3)=25