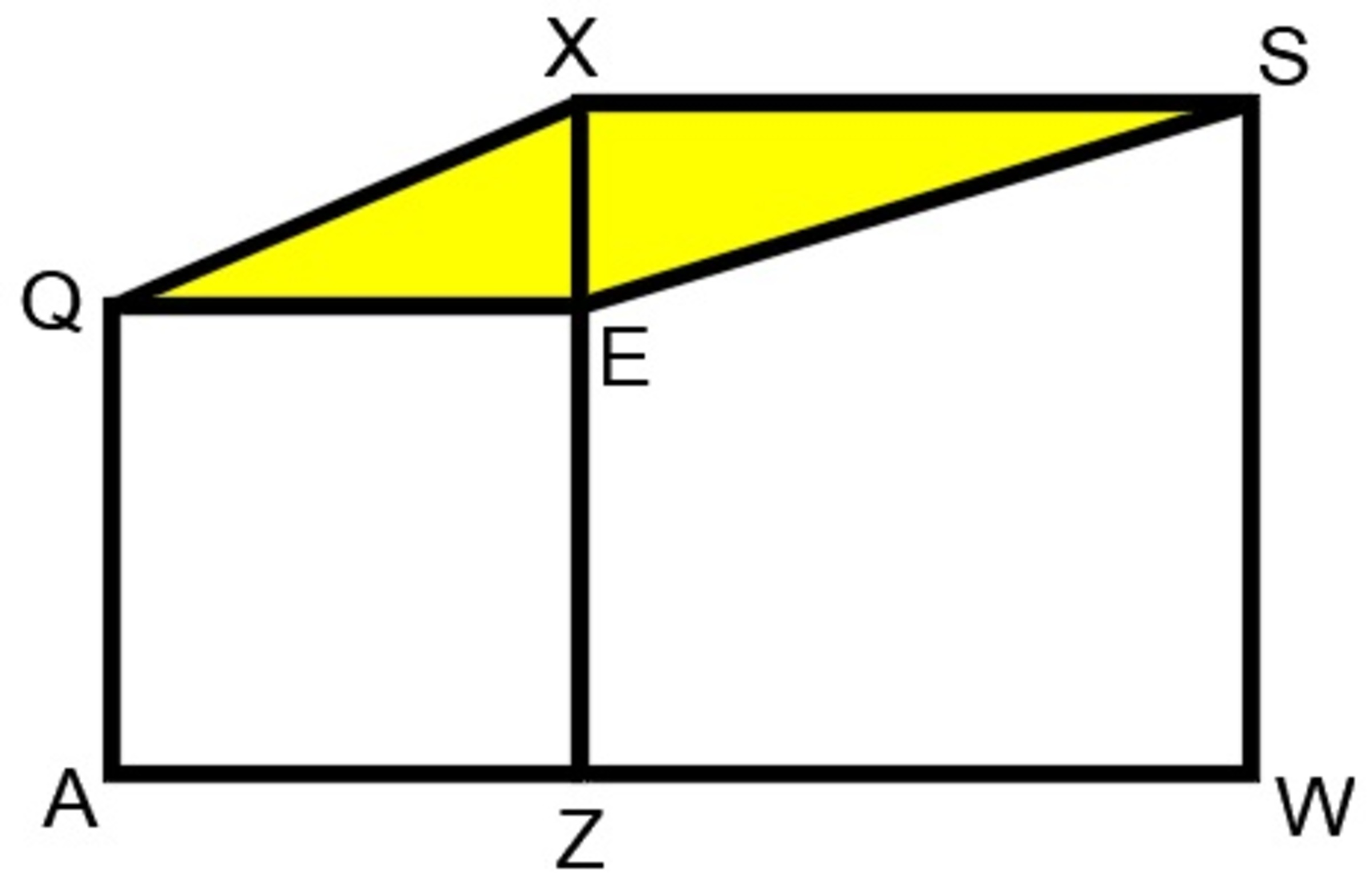
area of the shaded portion

Let $x = ZW$ , the side length of the larger square, and $y = AZ$ , the side length of the smaller square.

We are given $x^2 - y^2 = 273$ .

Now consider the area of the yellow trapezoid $XSEQ$ . (First, we must note that this is a trapezoid, since $\overline{QE} \| \overline{XS}$ .)

The area formula for a trapezoid is $A = \frac{(b_1 + b_2)h}{2}$ , namely the height times the average of the two base lengths.

Here $h = XE = (x -y)$ , $b_1 =XS = x$ and $b_2 = QE = y$ .

Thus,

$A = \frac{(x+y)(x-y)}{2} = \frac{x^2 - y^2}{2} = \frac{273}{2}.$