area of the shaded region
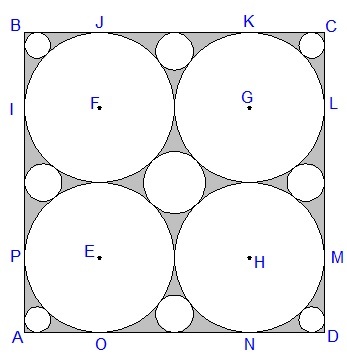 Four circles with centers
are fitted in square
as shown. If the side length of the square is
, find the area of the shaded region.
Four circles with centers
are fitted in square
as shown. If the side length of the square is
, find the area of the shaded region.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We have four groups of circles. The first group is the four big circles, each is obviously of radius R = 3 .
Next, we have a single circle in the middle. It radius r 1 can be deduced, by drawing the right triangle in the following figure. The triangle is an isosceles right triangle with side angles of 4 5 ∘ . Hence
2 R + 2 r 1 = 2 2 R .
from which, r 1 = 3 ( 2 − 1 ) .
Next, we consider the four smaller circles on the sides on the square, and we draw a right triangle as in the following figure.
From which, by applying the Pythagorian theorem, we obtain,
( R + r 2 ) 2 = ( R − r 2 ) 2 + R 2
Simplifying,
r 2 = 4 R = 4 3
Next, we consider the four smallest circles at the corners of the square, for which we draw a right triangle as shown in the figure below.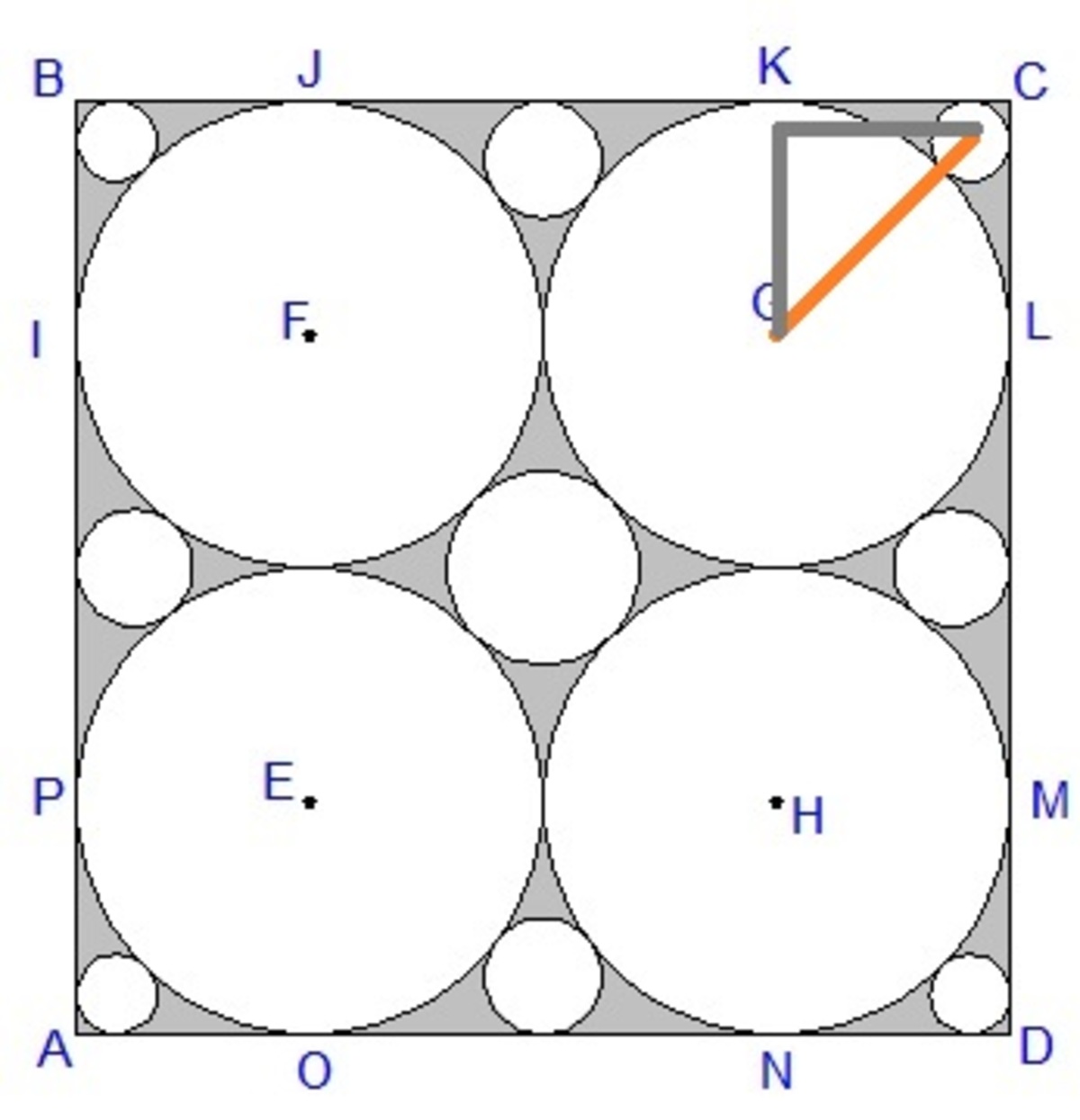
Since the triangle is an isosceles right triangle, we can write,
R + r 3 = 2 ( R − r 3 )
Solving for r 3 , we get,
r 3 = R 2 + 1 2 − 1 = 3 2 + 1 2 − 1 = 3 ( 3 − 2 2 )
The last expression was obtained by rationalizing the denominator.
We're almost done. The area of the gray region is the area of the square minus the area of all the circles.
Hence,
Area = 1 2 2 − π ( 4 R 2 + r 1 2 + 4 r 2 2 + 4 r 3 2 )
Substituting the values we obtained for r 1 , r 2 , r 3 , we obtain,
Area = 1 4 4 − π ( 3 6 + 9 ( 3 − 2 2 ) + 4 9 + 3 6 ( 1 7 − 1 2 2 )
Simplifying,
Area = 1 4 4 − π ( 6 7 5 + 4 9 − 4 5 0 2 )
And finally,
Area = 1 4 4 − 4 2 7 0 9 π + 4 5 0 2 π