Area of A Spinner
In the diagram, regular hexagon A B C D E F has sides of length 2 .
Using A , C , E as centers, portions of circles with radius 1 are drawn outside the hexagon.
Using B , D and F as centers, portions of circles with radius 1 are drawn inside the hexagon. These six circular arcs join together to form a curve. Determine the area of the shaded region, both red and green, enclosed by this curve.
Problem Courtsey: Waterloo University.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you for sharing a nice solution.
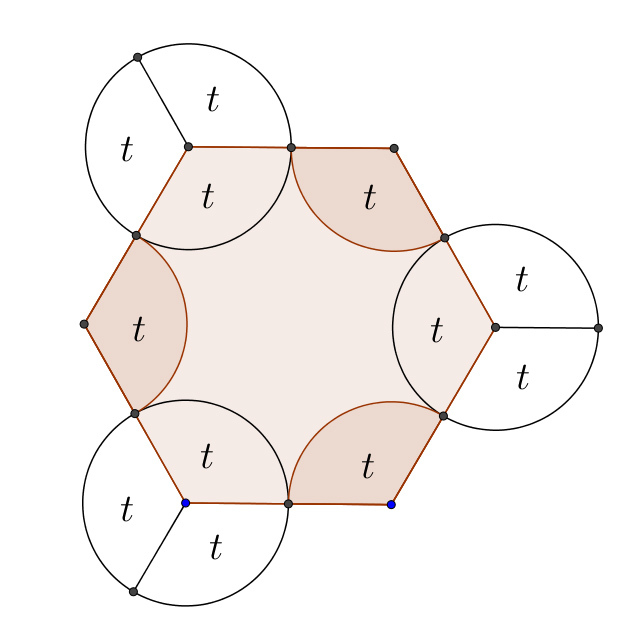
The area of the regular hexagon is: 2 3 a 2 ∗ 3 = 2 3 ∗ 4 ∗ 3 = 6 3 The shaded region (which looks like a fidget spinner :) ) is equal to the area of the hexagon + 3 sector with an area of t . Since three sector with an area of t define a circle with radii 2 2 = 1 , the area of the shaded region is: 6 3 + 3 t = 6 3 + r 2 ∗ π = 6 3 + 1 π = 6 3 + π
Thank you for sharing a nice solution.
Log in to reply
I loved this puzzle, because the shaded area is like a fidget spinner. This is a really 21th century puzzle ;)
Log in to reply
I knew it. My kids have spinners and when l saw this problem, l thought it would be nice to post something related to it.
let y be the area of the red region (1 part). One part is in the form of a sector of a circle. So
y = 3 6 0 2 4 0 π ( 1 2 ) = 3 2 π , since there are three parts, 3 y = 3 ( 3 2 ) π = 2 π
let x be the area of the white region (1 part). One part is in the form of a sector of a circle. So
x = 3 6 0 1 2 0 π ( 1 2 ) = 3 1 π , since there are three parts, 3 x = 3 ( 3 1 ) = π
let H be the area of the regular hexagon. Since a regular hexagon is composed of 6 equilateral triangles, we have
H = 6 ( 2 1 ) ( 2 2 ) ( 2 3 ) = ( 3 ) ( 4 ) ( 2 3 ) = 6 3
Let A be the area of the shaded part (red and green). then
A = H − x + y = 6 3 − π + 2 π = 6 3 + π