Area of the yellow region
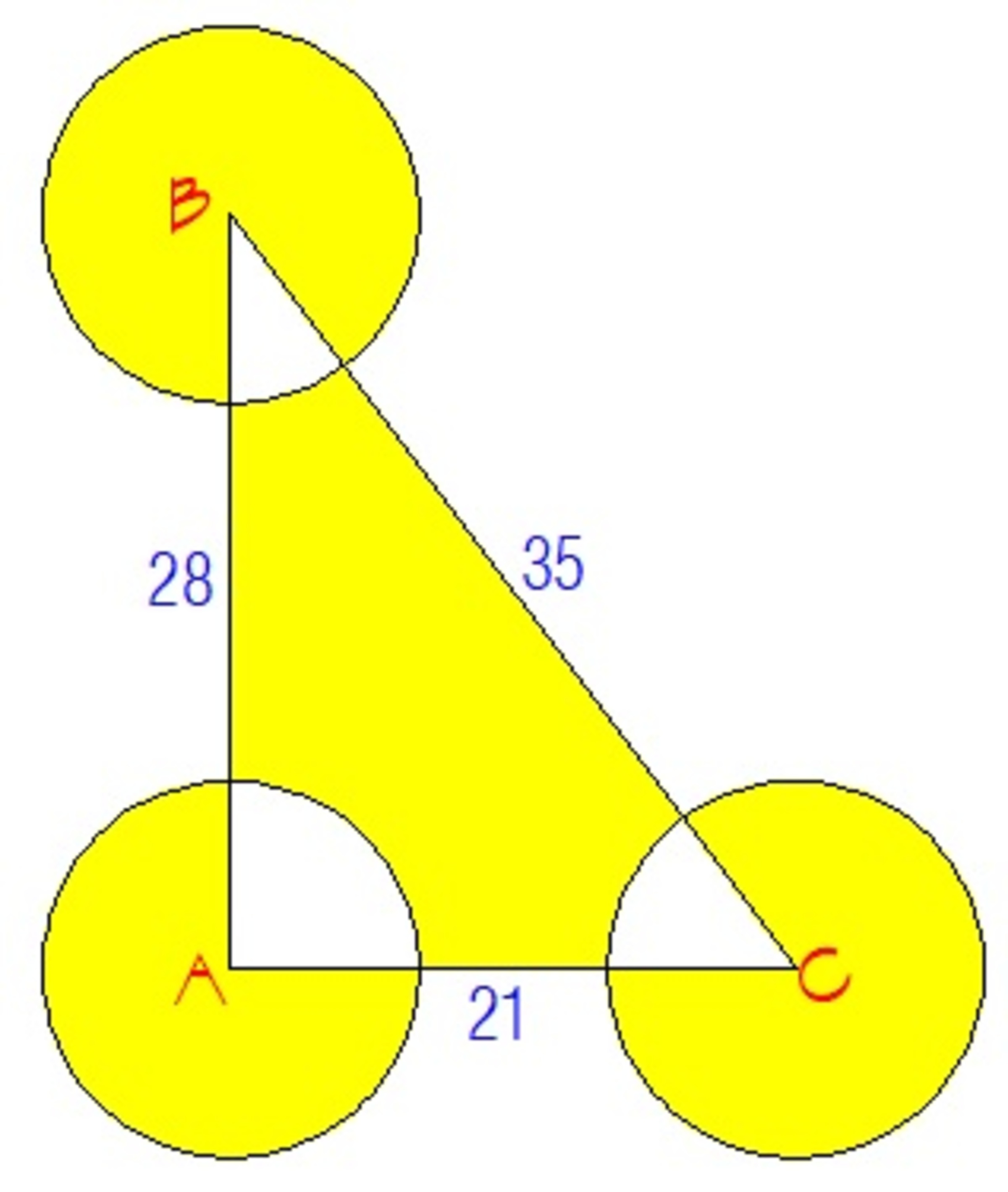 Triangle
A
B
C
is a right triangle with side lengths
2
1
,
2
8
and
3
5
. Three circles of radius
7
are drawn with centers at
A
,
B
and
C
, respectively. Find the area of the yellow region to the nearest integer. Use
π
=
7
2
2
.
Triangle
A
B
C
is a right triangle with side lengths
2
1
,
2
8
and
3
5
. Three circles of radius
7
are drawn with centers at
A
,
B
and
C
, respectively. Find the area of the yellow region to the nearest integer. Use
π
=
7
2
2
.
Note:
During calculation, maintain a precision of two decimal places.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The area of the yellow region is equal to the the sum of the areas of the three circles plus the area of the right triangle minus twice the sum of the areas of the three circular sectors.
tan B = 2 8 2 1 ⟹ B = tan − 1 2 8 2 1 ≈ 3 6 . 8 7 ∘
tan C = 2 1 2 8 ⟹ C = tan − 1 2 1 2 8 ≈ 5 3 . 1 3 ∘
A = 7 2 2 ( 7 2 ) ( 3 ) + 2 1 ( 2 1 ) ( 2 8 ) − 2 [ 4 1 ( 7 2 2 ) ( 7 2 ) + 3 6 0 3 6 . 8 7 ( 7 2 2 ) ( 7 2 ) + 3 6 0 5 3 . 1 3 ( 7 2 2 ) ( 7 2 ) ] ≈ 6 0 2
Since A + B + C = 180, the white arcs that have to be subtracted of the triangles form a half circle. The are thus equals: A(Triangle) - 0.5 A(circle) + 3 A(circle) - 0.5 A(circle) = A (Triangle) + 2 A(circle) = 0.5 28 21 + 22/7 * 49 * 2 = 602.
find area of yellow triangle .as sum of white angles is 180 and r is 7.area of white is 1/2 π 49=77.then find area of 3 circles. subtract 77 from it to get area of yellow region of circles.add all the areas of yellow region .